SOLUTION: Determine the present value of a series of 60 monthly payments of $2,500 each which begins 1 month from today. Assume interest of 10 percent per year compounded quarterly.

In this tricky problem, the monthly payments are not compounded. 


Monthly payments lie in the bank and wait for the end of a quarter - 
only then they are compounded, according to the problem.


So, we actually have quarterly payments of 3*2500 = 7500 dollars each, compounded quarterly.


Thus, it works as an Ordinary Annuity saving plan with quarterly payments of $7500 
at the end of each quarter, compounded quarterly at the annual rate of 10%.


60 monthly payments of $2500 each mean 60/3 = 20 quarterly payments of $7500 each.


So, the future value of the account after 20 quarters will be

    FV =  = 191584.93  dollars.


Now we want to find the present value X.  It is the starting value of the account,
which, when compounded quarterly at 10% per year, will have the same future value in 20 quarters.


So, we write this equation

    191584.93 = .


It gives the solution

    X = 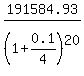 = 116918.72  dollars.


ANSWER.  The present value is $116918.72 dollars.