SOLUTION: You want to buy a $35,000 car. You can make a 10% down payment, and will finance the balance with a 4% interest rate for 48 months (4 years). What will your monthly payments be?

Algebra ->  Customizable Word Problem Solvers  -> Finance -> SOLUTION: You want to buy a $35,000 car. You can make a 10% down payment, and will finance the balance with a 4% interest rate for 48 months (4 years). What will your monthly payments be?       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1146251: You want to buy a $35,000 car. You can make a 10% down payment, and will finance the balance with a 4% interest rate for 48 months (4 years). What will your monthly payments be?
Found 2 solutions by Theo, math_tutor2020:
Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
10% of 3500 = 3500
subtract that from 35000 and you have to finance 31500.

use the following online financial calculator.
https://arachnoid.com/finance/

your inputs are:

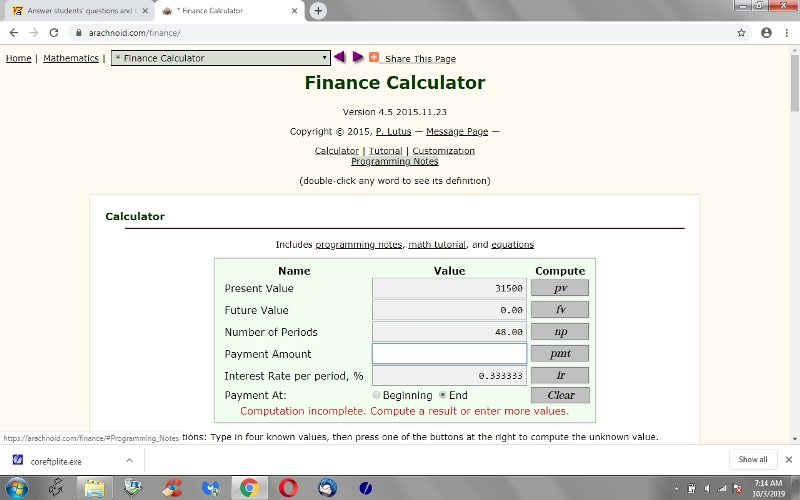
present value = 31500
future value = 0
number of time periods = 48 months
interest rate per time period = 4% per year / 12 = .33333333% per month.
payments are made at the end of each time period.

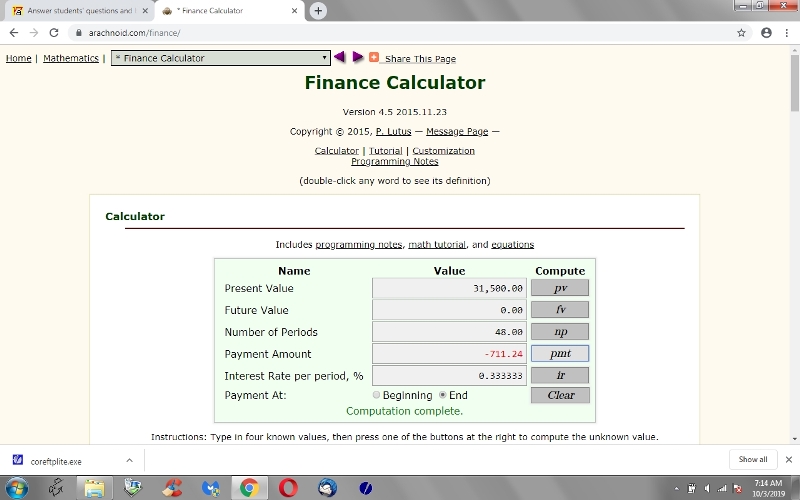
click on PMT and the calculator tells you that the payments at the end of each month need to be -711.24

the payments are shown as negative because the present value is positive.
if you entered the present value as negative, the payment would be shown as positive.
positive means money coming in.
negative means money going out.
you get the loan so the 31500 is money coming in.
you make the payments at the end of each month so the payments are shown as negative.

inputs are shown followed by the results after clicking on PMT.

$$$

$$$



Answer by math_tutor2020(3816) About Me  (Show Source):
You can put this solution on YOUR website!

If you are curious how @Theo got the correct answer of $711.24, then check out the steps below.

The formula to use is this
P = (L*i)/( 1-(1+i)^(-n) )
where,
P = monthly payment
L = 31,500 = loan amount (which is 90% of the 35000)
i = interest rate per month = 0.04/12
n = number of months = 48

So,
P = (L*i)/( 1-(1+i)^(-n) )
P = (31,500*0.04/12)/( 1-(1+0.04/12)^(-48) )
P = 711.24022121322
P = 711.24

Here are 2 other calculators that will help confirm the answer (they're basically the same with some slight differences)
https://www.calculator.net/loan-calculator.html
https://www.bankrate.com/calculators/mortgages/loan-calculator.aspx
Both of which are free.
There are tons more options of course, so feel free to use your favorite.

Answer: $711.24