Question 1143508: A businessman borrowed P3,000,000 with interest at the rate of 6% compounded annually. He agrees to discharge his obligations by paying series of 6 annual payment,the first being due at the end of the fifth year. Determine the value of his annual payment.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! he will make 6 payments at the end of each year starting from the end of the firth year.
the interest rate is 6% per year.
the present value of the loan is 3,000,000 at the end of year 0.
the end of year 0 is the same time point as the beginning of year 1.
the future value of this loan at the end of year 4 is equal to 3,000,000 * 1.06^4 = 3,787,430.88.
3,787,430.88 is the present value of the loan at the end of year 4.
the end of year 4 is the same time point as the beginning of year 5.
there are 6 annual payments starting at the end of year 5.
what you have, therefore, is the following inputs to a financial calculator.
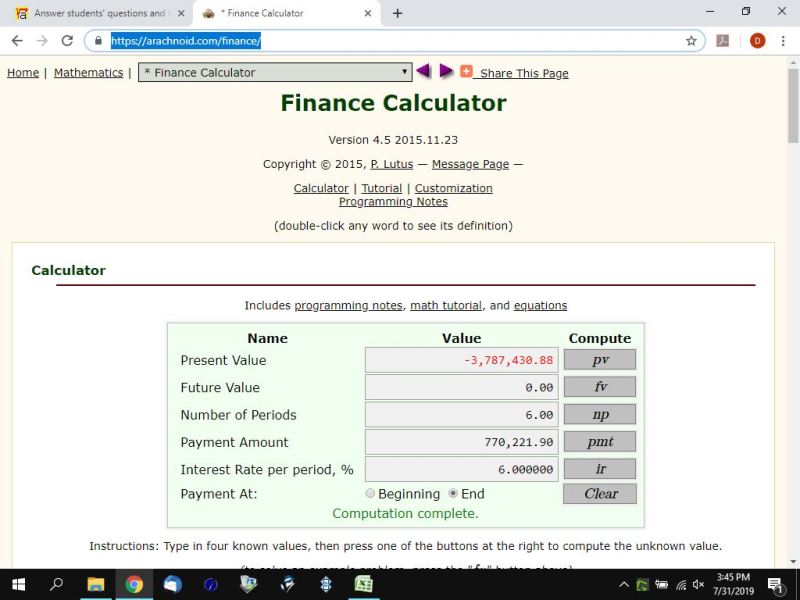
present value = 3,787,430.88.
future value = 0
number of time periods = 6
interest rate per time period = 6%
payments are made at the end of each time period.
the calculator then tells you that the payments at the end of year year need to be 770,221.90.
that is your solution.
the calculator i used can be found at https://arachnoid.com/finance/
here's a display of the results using this calculator.
i also did a cash flow analysis using excel.
here's a display of the results of that cash flow analysis.

boy means beginning of year.
eoy means end of year.
these are the time points.
the beginning of year 1 is the same time point as the end of year 0.
the beginning of year 5 is the same time point as the end of year 4.
column F is the loan
column G is the payments on that loan.
column H is the remaining balance of the loan.
the calculations for the remaining balance of the loan are:
the remaining balance of the loan at the end of year 0 is the loan itself.
the remaining balance of the loan at the end of yer 1 is the value of the loan at the end of year 0 * 1.06 minus any payment at the end of year 1.
this continues for each year.
at the end of year 5, the remaining balance of the loan is equal to value of the loan at the end of year 4 * 1.06 minus the value of the payment at the end of year 5.
this becomes $3,787,430.88 * 1.06 = $4,014,676.733 - $770,221.90 = $3,244,454.833, shown as $3,244,454.83.
this same procedure continues to the end of the loan period where the remaining balance is $.01.
it is actually $0.00 but there is a small error due to rounding of the payment amount.
the actual values, without rounding are:
|
|
|