SOLUTION: A man is planning to retire in 25 years. He wishes to deposit a regular amount every three months until he retires so that, beginning one year following his retirement, he will

    Different schemes are possible, and each such a scheme requires a separate consideration - but what I propose 

    is natural and reasonable, making the problem correctly and precisely formulated.

First, I will determine how much money X should be accumulated on the account during 25 years,
in order for to have enough to withdraw $32000 at the beginning of each of the next 10 years.


By withdrawing $32000 at the beginning of each year, the account (the remaining money) still earns 8% per annum compounded quarterly.


It means that effective annual rate for this account is 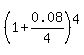  = 1.082432 compounded annually.


So, when you withdraw money during 10 years from your account, it still earns with effective rate of 1.082432 per year compounded annually.

Thus, it works as if it would be compounded annually at the rate of 8.2432%.


Such scheme withdrawing money was considered at the lesson  
    Withdrawing a certain amount of money periodically from a compounded saving account  
in this site.


The formula for the account value before it starts discharging is

    M = ,     (1)


which gives us the value at the account of

    M  = 212387 dollars.

Now I am in position to determine how much the person should deposit each quarter during 25 years 

to accumulate  212387 dollars in his account. The number of quarter periods is 25*4 = 100.


Now we have a standard Annuity saving plan, and the formula is

    212387 = 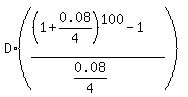,     (2)


where D is the quarterly deposit amount.


The multiplier 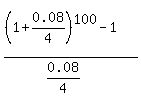   is equal  312.2323 ,  


which implies from equation (2)  that  D = 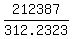 = 680.22.


It is your answer:  During 25 years the person should deposit $680.22 at the end of each quarter to his account,

                    in order to withdraw  $32000  at the beginning of each year during 10 years at given conditions.