SOLUTION: Find the periodic payment for each sinking fund that is needed to accumulate the given sum under the given conditions. (Round your answer to the nearest cent.) FV = $2,200,000, r

Algebra ->  Customizable Word Problem Solvers  -> Finance -> SOLUTION: Find the periodic payment for each sinking fund that is needed to accumulate the given sum under the given conditions. (Round your answer to the nearest cent.) FV = $2,200,000, r       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1140367: Find the periodic payment for each sinking fund that is needed to accumulate the given sum under the given conditions. (Round your answer to the nearest cent.)
FV = $2,200,000, r = 2%, compounded weekly for 15 years
ANY AND ALL HELP IS APPRECIATED! :)
Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
using my Texas Instruments Business Analyst II calculator, i do the following:

present value = 0
future value = 2200000
periodic payment = 0
interest rate per time period = 2% per year / 52 = .038461538% per week
number of time periods = 15 years * 52 = 780 weeks
payments are made at the end of each time period

i click on payment (PMT) and the calculator tells me that the payment at the end of each time period (end of each week) is equal to -2,419.096403.

the payment is shown as negative because it's money going out, while the 2,200,000 future value is shown as positive because it's money coming in.

you can do the same with the following online calculator.

https://arachnoid.com/finance/

here's a display of the result.

$$$

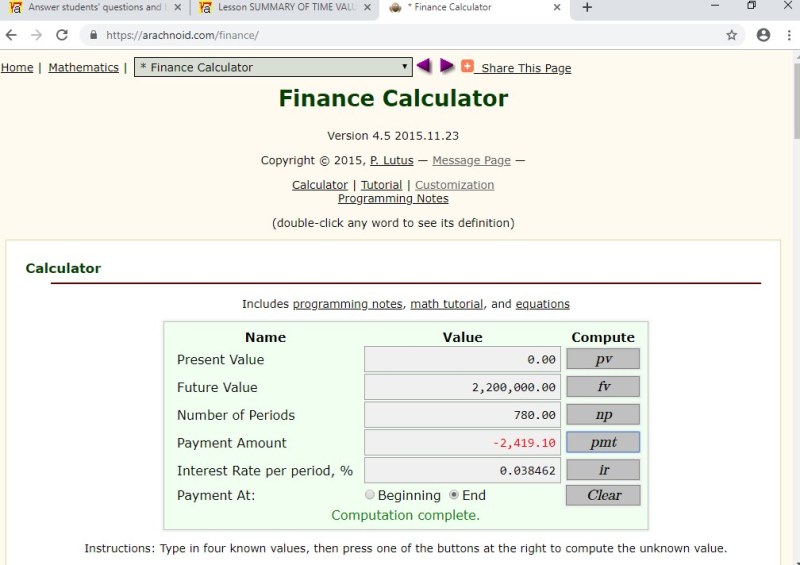
you can also do this by formula.

the formula is in the following reference.

https://www.algebra.com/algebra/homework/Finance/THEO-2016-04-29.lesson#f3

the particular formula to solve this kind of problem is shown below.

ANNUITY FOR A FUTURE AMOUNT WITH END OF TIME PERIOD PAYMENTS
a = (f*r)/((1+r)^n-1)
a is the annuity.
f is the future amount.
r is the interest rate per time period.
n is the number of time periods.

in this formula, the interest rate is the percent divided by 100 and all inputs are positive.

you still need to get the interest rate per time period and the number of time periods.

since the time periods are in weeks, you would do the following.

interest rate per time period = 2% / 100 = .02 per year / 52 = .0003846153846 per week.

number of time periods = 15 years * 52 weeks per year = 780 weeks.

your inputs to this formula are shown below.

a = (f*r)/((1+r)^n-1) becomes:

a = (2200000*.0003846153846)/((1+.0003846153846)^780-1)

the result is a = 2419.096404