|
Question 1140030: 1) A manufacture has been selling 1650 television sets a week at $540 each. A market survey indicates that for each $13 rebate offered to a buyer, the number of sets sold will increase by 130 per week.
a) Find the function representing the demand p(x), where x is the number of the television sets sold per week and p(x) is the corresponding price.
p(x)=
b) How large rebate should the company offer to a buyer, in order to maximize its revenue?
dollars
c) If the weekly cost function is 148500+180x, how should it set the size of the rebate to maximize its profit?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website!
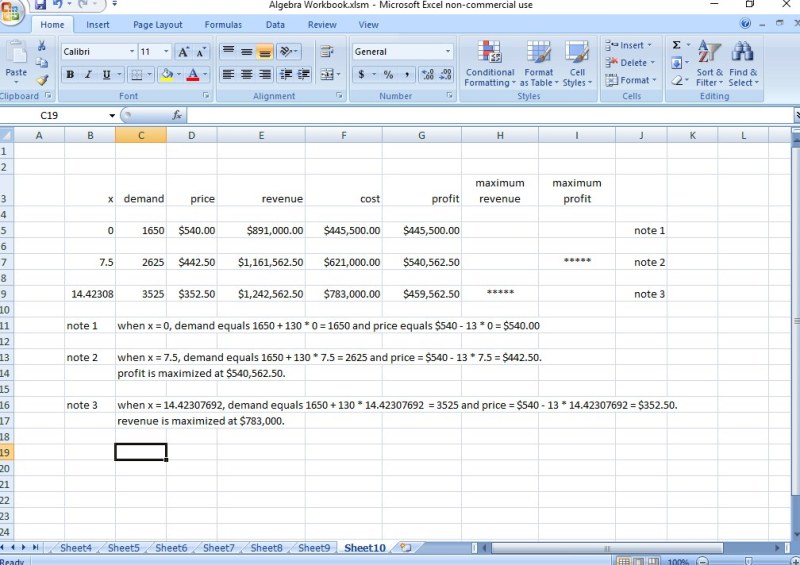
when your demand is 1650 and the price is 540, your revenue is equal to demand * price = 1650 * 540 = 891,000.
your cost is equal to 148,500 + 180 * the demand which becomes 148,500 + 180 * 1650 = 445,500.
your profit is then equal to revenue minus cost = 891,000 - 445,500 = 445,500.
you are given that, when the price goes down by 13 dollars a unit, the demand goes up by 130 units.
the equation for that is revenue = (1650 + 130 * x) * (540 - 13 * x).
the demand is (1650 + 130 * x) and the price per unit is (540 - 13 * x).
x does not represent the demand, nor does it represent the revenue.
130 * x represents the amount of change in the demand and 13 * x represents the amount of change in the price per unit.
when x = 0, the amount of change in the demand is 0 and the amount of change in the price is 0.
when x = 1, the amount of change in the demand is equal to plus 130 and the amount of change in the price is equal to minus 13 dollars.
when x = 2, the amount of change in the demand is equal to plus 260 and the amount of change in the price is equal to minus 26 dollars.
as such, x represents the number of increments of change in the demand and in the corresponding price.
it does not represent the demand itself.
this means that your cost equation, shown as 148500 + 180 * x, needs to be changed because the demand is represented by 1650 + 130 * x, and not x.
the cost equation becomes cost = 148,500 + 180 * (1650 + 130 * x).
you have a revenue equation equal to (1650 + 130 * x) * (540 - 130 * x).
you have a cost equation equal to 148,500 + 180 * (1650 + 130 * x).
since profit is equal to revenue minus cost, then your profit equation becomes:
profit = (1650 + 130 * x) * (540 - 130 * x) - (148,500 + 180 * (1650 + 130 * x)).
the revenue equation can be simplified to:
revenue = -1690x^2 + 48750x + 891000, which is a quadratic equation.
since it is in standard form, you get:
a = -1690
b = 48750
c = 891000
the maximum revenue occurs when x = -b/2a.
solve for x = -b/2a to get x = 14.42307692.
the maximum revenue is determined when you replace x in the revenue equation with 14.42307692.
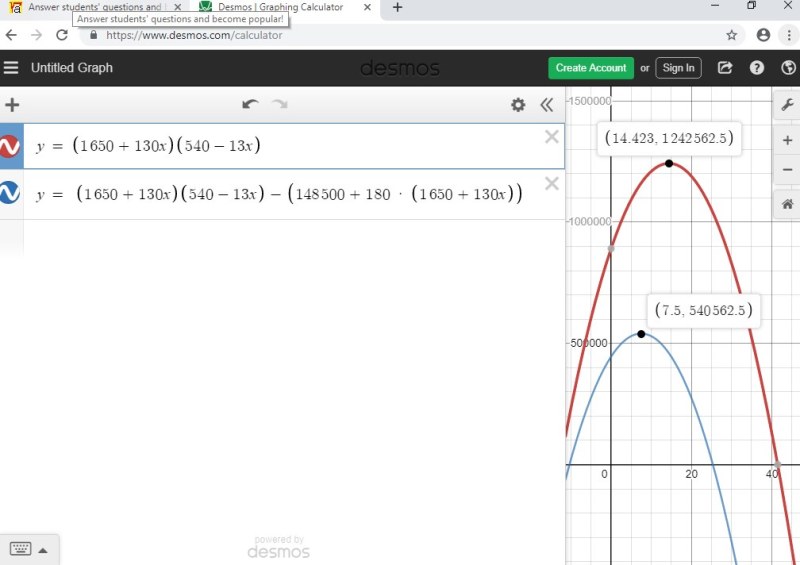
this gets you max revenue of 1,242,562.5 dollars.
the answer to question a is:
the revenue function is revenue = (1650 + 130 * x) * (540 - 13 * x)
the demand is represented by (165 + 130 * x)
the price is represented by (540 - 13 * x)
x represents the number of increments of change required.
the answer to question b is:
revenue is maximized when the rebate is equal to 13 * 14.42307692 = 187.5 dollars.
when x = 14.423076972, the demand is equal to 1650 + 130 * 14.42307692 = 3525 and the price is equal to 540 - 187.5 = 352.50 dollars.
the answer to question c is:
the profit is maximized when the rebate is equal to 13 * 7.5 = 97.5 dollars.
when x = 7.5, the demand is equal to 1650 + 130 * 7.5 = 2625 and the price is equal to 540 - 13 * 7.5 = 442.5 dollars.
the graph of the revenue and profit functions are shown below.
the display of the excel spreadsheet calculations are shown below.
|
|
|
| |