|
Question 1135512: Suppose you invest $140 at the end of each month for 5 years into an account earning 9% annual interest compounded monthly. After 5 years, you leave the money, without making additional deposits, in the account for another 28 years. How much will you have in the end?
Does anyone know how to solve this problem? I struggled all night to figure this out, and I still get it wrong. Thanks a bunch.
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52777)   (Show Source):
You can put this solution on YOUR website! .
It is ELEMENTARY . . .
STEP 1. Determine future value after first 5 years.
We have classic Ordinary Annuity saving plan (see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
in this site).
Future Value FV =  , (1)
where FV is the future value of the account; P is the monthly payment (deposit); r is the monthly percentage yield presented as a decimal;
n is the number of deposits (= the number of years multiplied by 12, in this case).
Under the given conditions, P = 140; r = 0.09/12; n = 12*5 = 60. So, according to the formula (1), you get at the end of the 5-th year
FV = 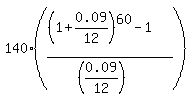 = = $10,559.38.
STEP 2. without making additional deposits, in the account for another 28 years.
FV = 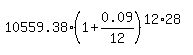 = 130,010 dollars.
ANSWER. At the end, the account will be $130,010.
Solved.
----------------
For Ordinary Annuity saving plans see my lessons I referred above.
Happy learning !
Answer by Theo(13342)  (Show Source):
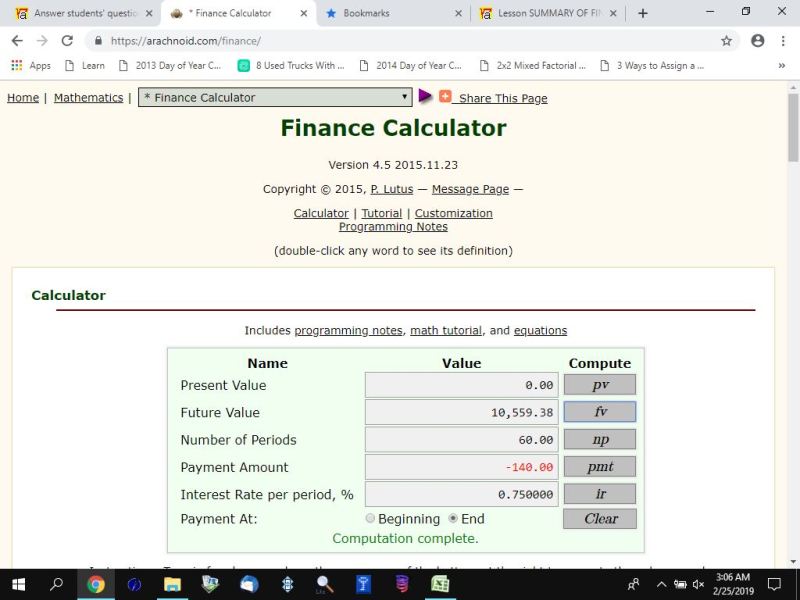
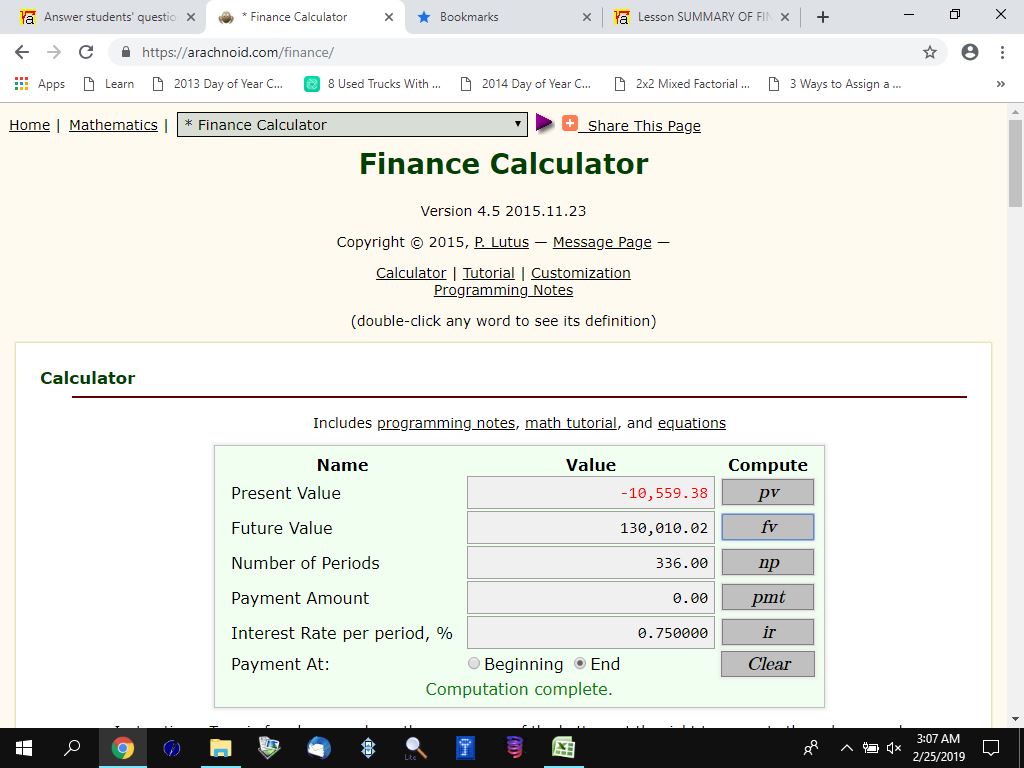
You can put this solution on YOUR website! if you use the following financial calculator, you will get the following results.
https://arachnoid.com/finance/
after 5 years, you will have $10,559.38.
28 years after that, you will have $130,010.02.
i also used the TI-BA-II Business Analyst calculator and got $130,010.01 without rounding the intermediate number of $10,559.38.
using the BA-II, that future value came out as 10,559.37917.
the online financial calculator rounded that to 10,559.38.
consequently, your answer could be 130,010.02 or it could be 130,010.02.
try those out and see how your do.
there are also manual formula that you can use, but i wouldn't bother with those unless you are absolutely required to use them.
most of the ones that apply are in the following reference.
https://www.algebra.com/algebra/homework/Finance/THEO-2016-04-29.lesson#notes
the first of these formulas you would use is:
FUTURE VALUE OF AN ANNUITY WITH END OF TIME PERIOD PAYMENTS
f = (a*((1+r)^n-1))/r
f is the future value of the annuity.
a is the annuity.
r is the interest rate per time period.
n is the number of time periods
a is equal to 140.
r is equal to 9/12 = .75 / 100 = .0075
n is equal to 5 * 12 = 60
solve for f to get f = 10559.37917
you would then take the future value result from formula and make it the present value of the following formula.
FUTURE VALUE OF A PRESENT AMOUNT
f = p*(1+r)^n
f is the future value.
p is the present amount.
r is the interest rate per time period.
n is the number of time period.
p is equal to 10559.37917
r is equal to .0075
n is equal to 28 * 12 = 336
solve for f to get f = 130010.0131
i also confirmed through excel that these figures are accurate.
here's the results of the excel analysis.
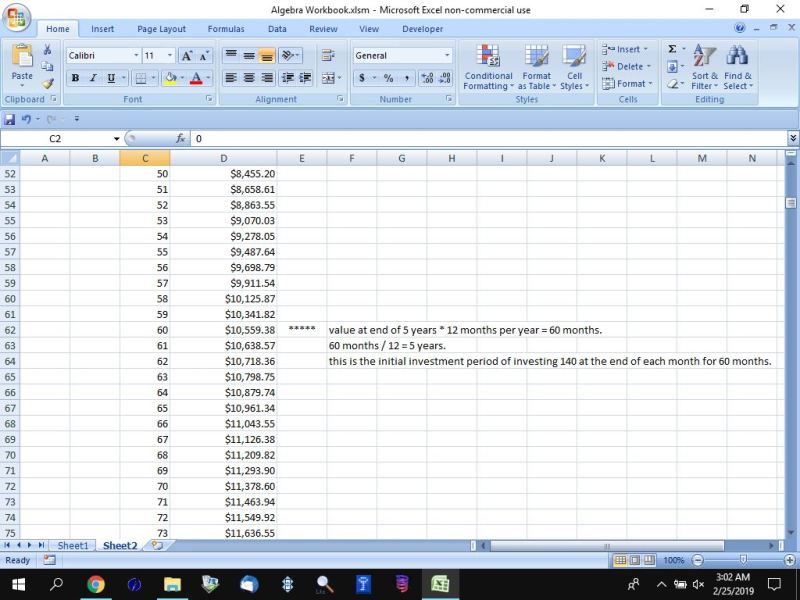
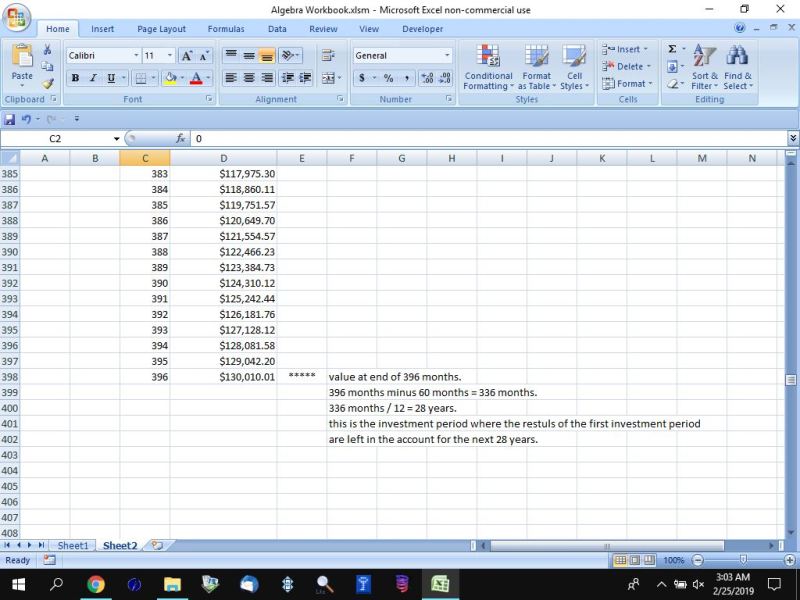
here's the results of the online calculator analysis.
|
|
|
| |
