SOLUTION: A rectangle has a length of 12 meters less than 2 times its width. If the area of the rectangle is 2574 square meters, find the length of the rectangle. ---- meters?

Click here to see ALL problems on Money Word Problems

Question 1134826: A rectangle has a length of 12 meters less than 2 times its width. If the area of the rectangle is 2574
square meters, find the length of the rectangle.

---- meters?
Found 5 solutions by addingup, MathTherapy, greenestamps, ikleyn, josgarithmetic:
Answer by addingup(3677)   (Show Source):
You can put this solution on YOUR website!
Area = L x W = 2574
L = 2W-12 substitute for L above:
2W-12 x W = 2574
2W^2-12W = 2574
2W^2-12W-5148 = 0
2(W^2-6W-2574) = 0
The easiest way would be by factoring. To do this, we multiply the coefficient of the 1st element times the constant: 1 x -2574 = -2574
Break down -2574 into its factors to see if we get to two factorswhose sum equals the coefficient of the middle term, which is -6:
-2574+1 = -2573
-1287+2 = -1285
-858+3 = -855
-429+6 = -423
-286+9 = -277
-234+11 = -223
etc.
.
If you continue, you will discover that there aren't two factors that would add to -6, so this trinomial cannot be factored.
Without wasting any more time, I will solve by completing the squares, a method which can solve all quadratic equations:
.
2W^2-12W = 2574 divide both sides by 2:
w^2-6W = 1287
now write the equation in the form x^2+2ax+a^2 = (x+a)^2:
2aW = -6W; 2a = -6; a = -3
add a^2 to both sides:
a^2 = -3^2 = 9
W^2-6W+(-3)^2 = 1287+(-3)^2
W^2+(-3)^2 = 1296
Complete the squares:
(W-3)^2 = 1296
W-3 = sqrt(1296)
W-3 = sqrt(36^2)
W-3 = 36
W = 39
.
W-3 = -sqrt(1296)
W-3 = -36
W = -33
.
I tried 39 in our equation 2W-12 x W = 2574 and it doesn't work. Let's try -33:
2W^2-12W = 2574
2(-33)^2-12(-33) = 2574
2(1089)+396 = 2574
2178+396 = 2574 Correct
.
Happy learning

Answer by MathTherapy(10551)   (Show Source):
You can put this solution on YOUR website!
A rectangle has a length of 12 meters less than 2 times its width. If the area of the rectangle is 2574
square meters, find the length of the rectangle.

---- meters?

Let width be W
Then length = 2W - 12
We then get: W(2W - 12) = 2,574

------ Factoring out GCF, 2

Factors of 1,287 that sum to - 6 are - 39 and + 33
(W - 39)(W + 33) = 0
W, or width = 39 m

For your sake, IGNORE EVERYTHING that @ADDINGUP wrote, especially the part where he tells you that the width is - 33 m. RIDICULOUS!!!

Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!

If you solve the problem using formal algebra, as in the solution by tutor @MathTherapy, you end up having to solve a quadratic equation by finding two numbers whose product is 1297, with one of the numbers 6 greater than the other.

If instead of the formal algebra you solve informally, working directly with the given information, you have to find two numbers whose product is 2574 and whose difference is 12. So you end up having to do the same kind of trial and error as with the formal algebra.

So there is no advantage to using formal algebra.

Tutor @addingup had the good idea to use this informal method for solving the problem; but he apparently overlooked the solution.

The prime factorization of the given area is

2574 = 2*2*3*11*13

A little playing around with these prime factors will find two factors of 2574 that satisfy the given condition (one is 12 less than twice the other) are 39 and 66.

So those are the dimensions of the rectangle; the length is 66m.

Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website!
.

            Let me show you the way that you, probably, NEVER HEARD and SEEN.

W is the width; (2W-12) is the length. The area equation is W*(2W-12) = 2574. (1) Multiply both sides by 2 to get 2W*(2W-12) = 5148. (2) Let x be the value midway between 2W and (2W-12) (the arithmetic mean of the two expressions). Then it is clear that 2W = x+6, while 2W-12 = x-6. Then the equation (2) becomes (x+6)*(x-6) = 5148 x^2 - 36 = 5148 x^2 = 5148 + 36 = 5184 ============> x = 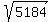= 72. Then 2W = x+6 = 72 + 6 = 78, hence, W = 78/2 = 39 and L = 2W-12 = 2*39 - 12 = 66. Answer. The length of the rectangle is 66 meters.

Solved and completed.

Notice that the only "time consuming" step in my solution was to take the square root of 5184.   //   Ha-ha-ha.

(The rest can be done MENTALLY).

-----------------

To see how this method/idea works in other similar problems, look into the lessons
    - HOW TO solve the problem on quadratic equation mentally and avoid boring calculations

    - Three methods to find the dimensions of a rectangle when its perimeter and the area are given
    - Three methods to find the dimensions of a rectangle when its area and the difference of two dimensions are given
in this site.

=============

Let me make my comment regarding the words by @greenestamps "there is no advantage to using formal algebra".

All what we teach you in this site, is formal algebra and/or is based on formal algebra methods. Thanks to those intellectual giants who built this base . . . If sometimes we tell you about possibilities to solve the problems mentally, it is not to convince you do not use formal algebra. We do it only to wider your horizon and/or to make your mind more flexible. So, do not consider these words by the esteem tutor @greenestamps too seriously . . . Consider them in a "joking mode" . . .

Answer by josgarithmetic(39616)   (Show Source):
You can put this solution on YOUR website!
L, length
w, width

-