Question 1113633: Best Motors has hired Robert Trent as its new president. Terms included the company’s agreeing to pay retirement benefits of $17,900 at the end of each semiannual period for 12 years. This will begin in 4,015 days. If the money can be invested at 8% compounded semiannually, what must the company deposit today to fulfill its obligation to Robert?
Found 3 solutions by solver91311, ikleyn, MathTherapy:
Answer by solver91311(24713)   (Show Source):
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
I will interpret the condition in this way:
1) We have first the period of 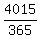 = 11 years, when the initial deposit of X dollars grows at 8% compounded semiannually.
2) Then the second period starts, when the company withdraw $17900 semiannually for 12 years to fulfill its obligation to Robert.
During this period of 12 years the rest of the account is still compounded at 8% semiannually,
and at the end of the 12 years period the amount vanishes.
The condition does not formulate all these details, so, from one side, it is my own interpretation / (fantasy).
From the other side, only this interpretation makes the problem really interesting, and it is major reason, why I start to work on it.
Solution
1. After 11 years, the initial deposit of X dollars becomes
P =  =  .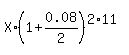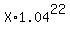
2. Then the following next 12 years period we have the ordinary annuity plane with the NEGATIVE semiannual deposit (= withdraw) of $17900.
So, the usual ORDINARY ANNUITY PLAN formula works with the negative deposit of 17900 dollars:
P =  =  .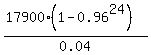
So your equation to find X is THIS:
=  .
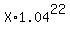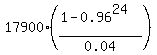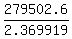x*2.369919 = 279502.6 =====> X =  = 117937.60.
Answer. Under the given condition and interpretation the initial deposit the company must make TODAY is 117937.60 dollars.
Solved.
----------------
See the lesson
- Ordinary Annuity saving plans and geometric progressions
in this site.
================
I absolutely agree with John in that you do not need copy your post many times - it only annoys/irritates the tutors and works against your best interests.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! Best Motors has hired Robert Trent as its new president. Terms included the company’s agreeing to pay retirement benefits of $17,900 at the end of each semiannual period for 12 years. This will begin in 4,015 days. If the money can be invested at 8% compounded semiannually, what must the company deposit today to fulfill its obligation to Robert?
If the interest rate of 8% were to remain the same, amount needed to pay out $17,900 every 6 months for 12 years, or for 24 periods, would be: $272,920.64.
This is your FUTURE VALUE, or the amount needed in 4,065 days, or in 
The PRESENT VALUE, based on a FUTURE VALUE of $272,920.64, an interest rate of 8%, semi-annual compounding periods, and time of 11 years ( ) =  .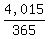
This is the required deposit, TODAY!!
|
|
|
