Question 1113167: Brian Costa deposited $20,000 in a new savings account at 12% interest compounded semiannually. At the beginning of year 4, Brian deposits an additional $30,000 at 12% interest compounded semiannually. At the end of 6 years, what is the balance in Brianís account?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! he deposits 20,000 at 12% interest compounded semi-annually.
at the beginning of year 4, he deposits an additional 30,000 at 12% compounded semi-annually.
what is the balance in the account at the end of year 6?
formula to use is f = p * (1 + r) ^ n
f is the future value
p is the present value
r is the interest rate per time period
n is the number of time periods
your interest rate is 12% per year compounded semi-annually.
therefore the periods are semi-annual periods.
to find the interest rate per time period, take 12% and divide it by 2 compounding periods per year to get 6% per semi-annual period.
in the formula, it is entered as .06, which is the rate, not the percent rate.
the number of years needs to be multiplied by 2 to get number of semi-annual periods.
your first investment is for 6 years, therefore, you are talking 12 semi-annual periods.
your second investment is for 3 years, therefore, you are talking 6 semi-annual periods.
the formula is, once again:
f = p * (1 + r) ^ n
you get 2 formulas.
first formula is f = 20,000 * (1 + .06) ^ 12.
the second formula is f = 30,000 * (1 + .06) ^ 6.
the total money at the end of the 6th year is:
20,000 * (1 + .06) ^ 12 plus 30,000 * (1 + .06) ^ 6.
this results in a total amount at the end of the 6th year equal to 82799.5028
the spreadsheet output below gives you an idea of what the time period to time period cash flows look like.
your first investment is made at the beginning of the first year, therefore it is entered in time period 0, which is the beginning of the first year.
your second investment is made at the beginning of the fourth year, therefore it is entered in time period 8 which is the end of the third year and the beginning of the fourth year.
the year by year cash flow and future value of cash flow and cumulative sum of future value of cash flow is shown below.
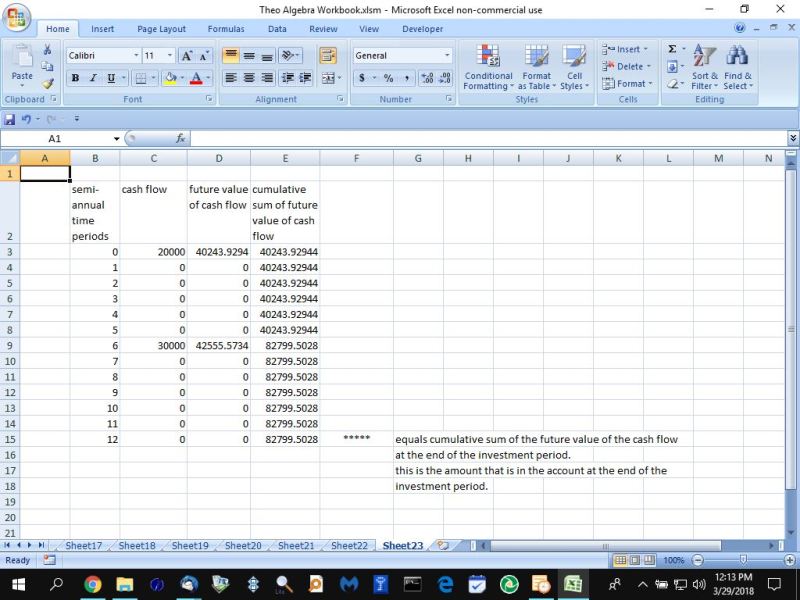
the trick in the cash flow is to get the time periods right.
the following table describes what they represent.
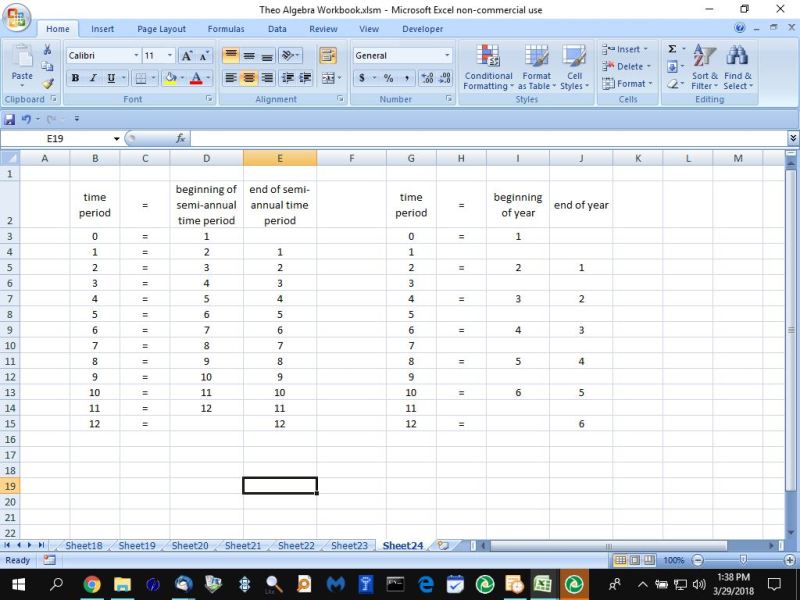
|
|
|