Question 1111534: My teacher didn't give me any formulas for these things.. please help me!! T~T
1. You can afford a $800 per month mortgage payment. You've found a 30 year loan at 6% interest.
a) How big of a loan can you afford?
b) How much total money will you pay the loan company?
c) How much of that money is interest?
2. How much would you need to deposit in an account now in order to have $2000 in the account in 15 years? Assume the account earns 3% interest compounded monthly.
3. You deposit $400 in an account earning 8% interest compounded annually. How much will you have in the account in 20 years?
4. You deposit $6000 in an account earning 3% interest compounded continuously. How much will you have in the account in 10 years?
5. You have $2,500 on a credit card that charges a 23% interest rate. If you want to pay off the credit card in 4 years, how much will you need to pay each month (assuming you don't charge anything new to the card)?
6. You deposit $500 in an account earning 5% coumpound interest for 4 years. Find the future value and the interest earned for each of the following compounding frequencies.
Future Value Interest Earned
Frequency
Annually:
Semiannually:
Quarterly:
Monthly:
Daily:
7. Gabriel and Paige have a new grandson. How much money should they invest now so that he will have $52,000 for his college education in 18 years? The money is invested at 2.8% compounded quarterly.
8. You owe $15,000 on student loans at an interest rate of 4.65% compounded monthly. You want to pay off the loan in 13 years.
a. What will your monthly payments be?
b. How much interest do you pay?
9. You decide to quit using your credit card and want to pay off the balance of $5,800 in 3 years. Your interest rate is 19.85% compounded monthly.
a. What will your monthly payments be?
b. How much interest do you pay?
10. You want to buy a $171,000 home. You plan to pay 15% as a down payment, and take out a 30 year loan at 5.35% interest for the rest.
a) How much is the loan amount going to be?
b) What will your monthly payments be?
c) How much of the first payment is interest?
11. You want to buy a $242,000 home. You plan to pay 10% as a down payment, and take out a 30 year loan at 5.45% interest for the rest.
a) How much is the loan amount going to be?
b) What will your monthly payments be?
c) How much total interest do you pay?
d) Suppose you want to pay off the loan in 15 years rather than 30. What will your monthly payment be?
e) How much money in interest will you save if you finance for 15 years instead of 30 years?
12. You want to buy a $140,000 home. You plan to pay 20% as a down payment, and take out a 30 year loan at 6.85% interest for the rest.
a) What is the amount of the down payment?
b) What will the amount of the mortgage?
c) The bank charges 1.5 points on the loan. What is the amount charged for points?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.
a) You can afford a  loan (rounding to the nearest cent). loan (rounding to the nearest cent).
b) You will pay the loan company 
c)  of that money is interest. of that money is interest.
To do that type of calculations, I see three options:
to use a factor from a table, or
to use software, or
to use a formula.
In the past, I have seen real estate salespeople look up the monthly payment per $1000 of mortgage loan, given the number of years for the loan. Nowadays, they probably calculate it using a computer, or a specialized app, or a financial calculator.
To find the answer to 1a), I used the function PV (present value) in a Microsoft Excel spreadsheet,
entering  as Rate (per month, and in decimal form), as Rate (per month, and in decimal form),
 for Nper (the number of periods, or equal payments), for Nper (the number of periods, or equal payments),
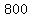 for PMT (the amount of each payment), for PMT (the amount of each payment),
 for FV (future value), for FV (future value),
and 0 (no entry) for "Type" (meaning payments made at the end of each period).
I got the same number from the spreadsheet calculating
 . .
(For accuracy, I carry a lot of digits, to round to less total number of digits later).
That was my solution to an equation with the numbers for this problem.
As a formula, it would be  . .
If you can read algebra, following order of operations conventions,
you can use that formula.
The formula above may not be the formula in a book,
but it is one that can be deduced using algebra.
You would need to know enough math to realize that
  
You would alzo need realize that to get form an intially owed amount  , ,
to a zero balance after  payments, payments,
when interest of 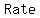 is applied to is applied to
the balance at the end of each payment period,
just before the payment  is applied, is applied,
it must be





2
Interest is called compounded when
interest is added to the prior balance
at the end of every compounding period
(every year, every quarter, every month, every day,etc),
and then the larger balance earns interest for the next compounding period.
For an initially deposit amount  (usually called principal), (usually called principal),
and an annual rate  expressed as a decimal, expressed as a decimal,
compounded  times a year, times a year,
after  years, the final balance (Future value, FV}}} would be years, the final balance (Future value, FV}}} would be

If an account earns 3% annual interest compounded monthly,
an initial amount  earns earns  each month. each month.
(In decimal form, the interest rate is  per year, per year,
or  per month) . per month) .
The interest earned the first month is  . .
On the second month, the account earns interest on a balance of
 . .
The balance gets multiplied by  during the second month, during the second month,
and every month thereafter.
There are  compounding periods (months) in a year. compounding periods (months) in a year.
After  years, years,  months, months,
the balance is  . .
If that final balance must be 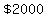 , ,
it must be  . .
Solving for  , you find that , you find that
the amount that needs to be deposited at the beginning of those 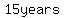 is is
  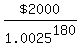  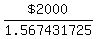  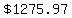 (rounding to the nearest cent). (rounding to the nearest cent).
3.
For this problem, interest is compounded  time per year, time per year,
 , ,  and and  . .
With an account earning 8% interest compounded annually,
 of the initial amount of the initial amount
is added to the balance at the end of each year period.
Then new balance is  times the balance of 1 year before. times the balance of 1 year before.
After  , the initial deposit is multiplied times , the initial deposit is multiplied times  . .
If the initial deposit is 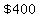 , ,
after 20 years it will have grown to
 (rounding to the nearest cent). (rounding to the nearest cent).
4.
As the number of compounding periods in a year becomes larger and larger,
the factor  that tells you how much the initial deposit that tells you how much the initial deposit 
has grown in 1 year increases, but there is a limit.
That limit is 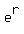 , where , where  is an irrational number is an irrational number
that is even to visualize than  . .
Interest that growth balances that way is said to be "compounded continuously."
After  years of continuous compounding at an annual rate years of continuous compounding at an annual rate  , ,
an initial deposit  will have grown to a balance of will have grown to a balance of

If you deposit  in an account earning 3% interest in an account earning 3% interest  compounded continuously, after compounded continuously, after  years you will have a balance of years you will have a balance of
 (rounding to the nearest cent). (rounding to the nearest cent).
5.
Assuming you don't charge anything new to the card,
it is like having a mortgage loan of $2,500,
to be paid in 4 years, with an annual interest rate of  . .
To find the answer, I could use the function PMT (payment) in a Microsoft Excel spreadsheet,
PV (present value)
entering  as Rate (per month, and in decimal form), as Rate (per month, and in decimal form),
 for Nper (the number of periods, or equal payments), for Nper (the number of periods, or equal payments),
 for PV (present value), for PV (present value),
 for FV (future value), for FV (future value),
and 0 (no entry) for "Type" (meaning payments made at the end of each period).
The result Excel gives me is 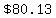
6.  in an account earning in an account earning   . .
The future value is  (see formula above), (see formula above),
and the interest earned is 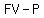
For each of the following compounding frequencies,  is is
Annually: 
Semiannually: 
Quarterly: 
Monthly: 
Daily:  . .
|
|
|