Question 1105261: The Fiedler family has up to $130,000 to invest. They decide that they want to have at least $40,000 invested in stable bonds yielding 5.5% and that no more than $60,000 should be invested in more volatile bonds yielding 11%. How much should they invest in each type of bond to maximize income if the amount in the stable bond should not exceed the amount in the more volatile bond? What is the maximum income?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! he will maximize his interest when he invests 70,000 at 5.5% interest and 60,000 at 11% interest.
his interest will be .055 * 70,000 + .11 * 60,000 = 10,450.
i solved this graphically using the desmos.com calculator.
my objective function was .055 * x + .11 * y which i wanted to maximize.
my constraint functions were:
x + y <= 130,000
x >= 40,000
y <= 60,000
x represented the amount invested at 5.5%.
y represented the amount invested at 11%.
two other constraints are that x and y are greater than or equal to 0.
my constraint functions then became:
x >= 40,000
y <= 60,000
x >= 0
y >= 0
using desmos, i graph the opposite of these constraints and then found the area on the graph what was not shaded.
that was the region of feasibility.
the corner points of this region are where the maximum interest would be located.
those corner points were at (40,000,60,000), (70,000,60,000), (130,000,0).
the objective function was evaluated at each of these corner points.
the maximum interest was at the point (70,000,60,000).
all the constraints were met at that corner point.
x was >= 40,000.
y was <= 60,000.
x + y was <= 130,000.
here's what the graph looked like.
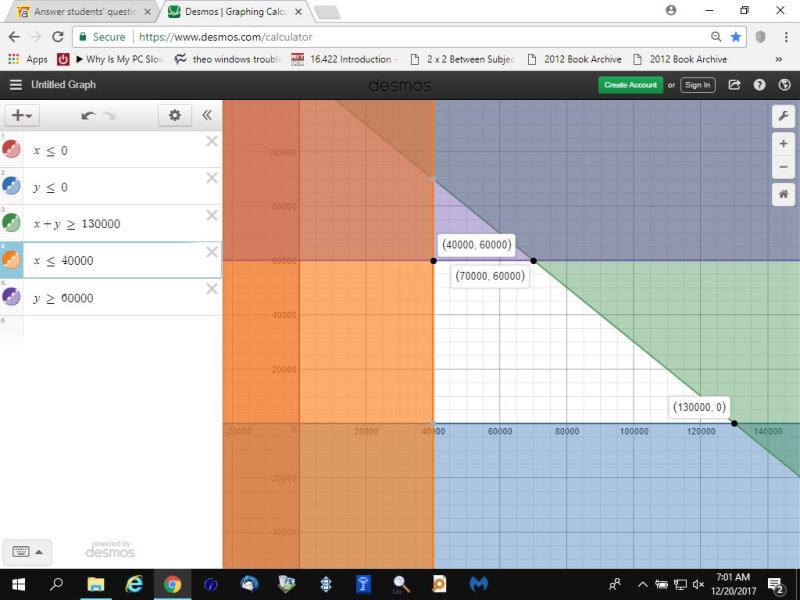
|
|
|