|
Question 1105248: Joely's Tea Shop, a store that specializes in tea blends, has available 45 pounds of A grade tea and 70 pounds of B grade tea. These will be blended into 1 pound packages as follows: A breakfast blend that contains one third of a pound of A grade tea and two thirds of a pound of B grade tea and an afternoon tea that contains one half pound of A grade tea and one half pound of B grade tea. If Joely makes a profit of $1.50 on each pound of the breakfast blend and $2.00 profit on each pound of the afternoon blend, how many pounds of each blend should she make to maximize profits? What is the maximum profit?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! without any other consideration, the maximum revenue points on the graph = (0,90), (75,40), (105,0).
these are the corner points of the feasible region.
you evaluate the objective function at these points to find the point that gives you the maximum profit.
the objective function is 1.5 * x + 2 * y
x represents the morning blend.
y represents the afternoon blend.
at the maximum point, all the constraints need to be satisfied.
the constraints are a maximum of 45 pounds of grade A tea and a maximum of 70 pounds of grade B tea.
the morning blend uses 1/3 of a pound of grade A and 2/3 of a pound of grade B tea.
the afternoon blend uses 1/2 of a pound of grade A and 1/2 of a pound of grade B tea.
grade A tea is therefore used at a rate of 1/3 of a pound for each pound of morning blend and 1/2 of a pound for each pound of afternoon blend.
the constraint equation for grade A tea is therefore:
1/3 * x + 1/2 * y <= 45
grade B tea is therefore used at a rate of 2/3 of a pound for each pound of morning blend and 1/2 of a pound for each pound of afternoon blend.
the constraint equation for grade B tea is therefore:
2/3 * x + 1/2 * y <= 70
in summary:
your objective function is 1.5 * x + 2.0 * y.
this represents the profit that you want to maximize.
your constraint functions are:
1/3 * x + 1/2 * y <= 45
2/3 * x + 1/2 * y <= 70
it helps to make a table, so you can see how these interact easier.
your table would look something like this:
morning blend afternoon blend total
variable x y
grade A tea 1/3 1/2 <= 45
grade B tea 2/3 1/2 <= 70
profit 1.5 2.0 maximize
the columns are the blends you are making (morning or afternoon).
the rows show you the constraints and the objective function.
from this table, you can easily see that grade A constraints are 1/3 * x + 1/2 * y <= 45 and 2/3 * x + 1/2 * y <= 70.
you can also see that the objective function is 1.5 * x + 2 * y and the objective is to maximize the profit.
there are additional constraints that x and y have to be >= 0 because they can't be negative.
using the desmos.com calculator, you would graph the OPPOSITE of the constraints and then evaluate the objective function at the corner points of the feasible region.
your feasible region is the area on the graph that is NOT shaded.
you would graph:
1/3 * x + 1/2 * y >= 45
2/3 * x + 1/2 * y >= 70
x <= 0
y <= 0
your graph would look like this:
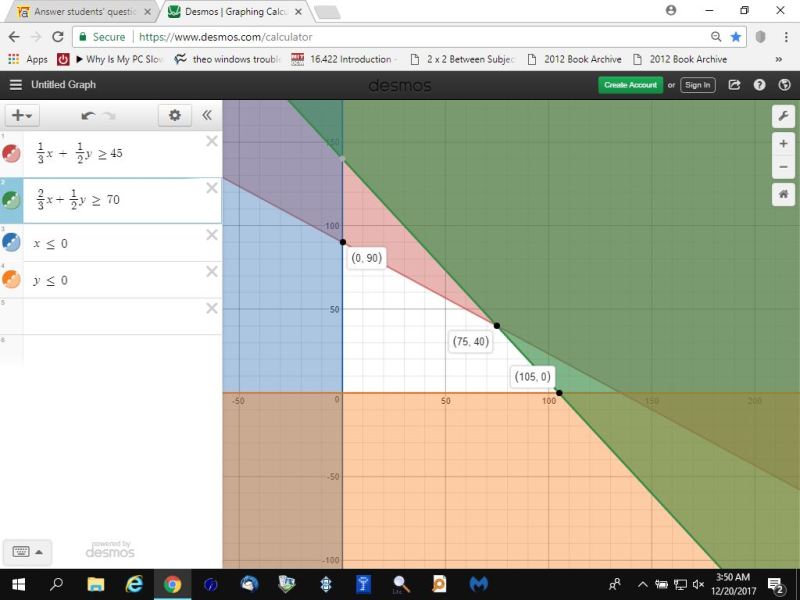
your maximum profit is at the (x,y) coordinate of (75,40).
at this corner point:
your profit is 75 * 1.5 + 40 * 2 = 192.5 dollars
your use of grade A tea is 75 * 1/3 + 1/2 * 40 = 45 pounds.
your use of grade B tea is 75 * 2/3 + 1/2 * 40 = 70 pounds.
note that using the demos.com calculator mechanizes the graphing of inequalities better than a lot of other calculator.
without the use of the desmos.com calculator, you would more then likely have to:
*** solve each equation for y prior to graphing.
*** graph the equality portion of all the inequalities.
*** manually find and shade the region of the graph that satisfies the inequalities.
this will get you the same answer, but involved more manual labor on your part.
i use the desmos.com calculator because it's much quicker once you learn how to use it properly.
this means being able to scale it so you get a clear picture of the feasible region.
it takes a while to learn, so it's perhaps notas easy as it sounds.
just remember:
using it the way that i do:
you graph the opposite of the inequalities and then find the area on the graph that is not shaded.
using a regular calculator that doesn't have this capability, then you:
graph the equality portion of the constraints.
find the area of the graph that satisfies the inequalities.
shade that region.
an example of graphing the equality portion of the constraints is:
the constraint of 1/3 * x + 1/2 * y <= 45 would be graphed as:
1/3 * x + 1/2 * y = 45.
|
|
|
| |