Question 1056090: On the opening night of a play at a local theater, 992 tickets were sold for a total of $11,680. Adult tickets cost $14 each. Children's tickets cost $11 each, and senior citizen tickets cost $8 each. If the combined number of children and adult tickets exceeded twice the number of senior citizen tickets by 287, then how many tickets of each type were sold?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
You can put this solution on YOUR website! x child tickets
y adult tickets
z senior tickets

You might want to try to first eliminate z, simplify the system to linear equations in x and y; and continue onward to finish. Alternatively, you could use other standard matrix row reductions or choose substitution method.
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website! On the opening night of a play at a local theater, 992 tickets were sold for a total of $11,680. Adult tickets cost $14 each. Children's tickets cost $11 each, and senior citizen tickets cost $8 each. If the combined number of children and adult tickets exceeded twice the number of senior citizen tickets by 287, then how many tickets of each type were sold?
Let number of adult, children, and senior citizen tickets sold, be A, C, and S, respectively
Then we get: A + C + S = 992 -------- eq (i)
Also, 14A + 11C + 8S = 11,680 ------- eq (ii)
And, A + C - 2S = 287 ------- eq (iii)
3S = 705 ------ Subtracting eq (iii) from eq (i)
S, or 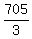 , or , or 
A + C + 235 = 992 _----- Substituting 235 for S in eq (i)
A + C = 992 - 235_____A + C = 757_____A = 757 - C ----- eq (iv)
14(757 - C) + 11C + 8(235) = 11,680 ---- Substituting 757 - C for A, and 235 for S in eq (ii)
10,598 - 14C + 11C + 1,880 = 11,680
- 14C + 11C + 12,478 = 11,680
- 3C = 11,680 - 12,478
- 3C = - 798
C, or 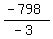 , or , or 
A = 757 - 266 ------ Substituting 266 for C in eq (iv)
A, or 
|
|
|