|
Question 1053338: The value of the dimes is exactly half the value of the quarters. The value of the nickels is 50 cents less than the value of the dimes. The value of the pennies is exactly half the value of the nickels. There are 97 coins in all with a combined value of $6. How much in quarters?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The value of the dimes is exactly half the value of the quarters. The value of the nickels is 50 cents less than the value of the dimes.
The value of the pennies is exactly half the value of the nickels. There are 97 coins in all with a combined value of $6.
How much in quarters?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let D be the value of dimes, in cents. (Notice: D is the VALUE, not the number of dimes !)
Then the value of quarters is 2D, according to the condition.
Then the value of nickels is (D-50), according to the condition.
Then the value of nickels is 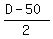 .
Then the combined value of all coins is
D + 2D + (D-50) + .
Then the combined value of all coins is
D + 2D + (D-50) + 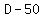 = 600.
dimes quarters nickels cents
You have ONE equation for only ONE single unknown D.
To solve it, multiply both sides by 2. You will get
2D + 4D + 2(D-50) + (D-50) = 1200.
Simplify it:
9D - 150 = 1200 ---> 9D = 1200 + 150 ---> 9D = 1350 ---> D = = 600.
dimes quarters nickels cents
You have ONE equation for only ONE single unknown D.
To solve it, multiply both sides by 2. You will get
2D + 4D + 2(D-50) + (D-50) = 1200.
Simplify it:
9D - 150 = 1200 ---> 9D = 1200 + 150 ---> 9D = 1350 ---> D = 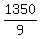 = 150.
Thus we found that the value of dimes is 150 cents. Hence, there are = 150.
Thus we found that the value of dimes is 150 cents. Hence, there are 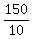 = 15 dimes in the collection.
Then the value of quarters is twice of it, i.e. 300 cents. Hence, the number of quarters is = 15 dimes in the collection.
Then the value of quarters is twice of it, i.e. 300 cents. Hence, the number of quarters is 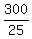 = 12.
So, we are ready to formulate the answer.
Answer. The number of quarters is 12.
Check. The value of nickels is D-50 = 150-50 = 100. Hence, the number of nickels is = 12.
So, we are ready to formulate the answer.
Answer. The number of quarters is 12.
Check. The value of nickels is D-50 = 150-50 = 100. Hence, the number of nickels is  = 20.
The value of cents is = 20.
The value of cents is 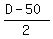 = = 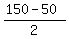 = 50. Hence, there are 50 1-cent coins.
In total, there are 15 + 12 + 20 + 50 = 97 coins. Correct! = 50. Hence, there are 50 1-cent coins.
In total, there are 15 + 12 + 20 + 50 = 97 coins. Correct!
The problem is solved.
The lessons to learn from the solution are:
1. This problem is for ONE unknown, not for 4 or 5.
2. The condition regarding the total number of coins is, actually, excessive. We can solve the problem without this condition.
3. The way proposed by the person "josgarithmetic" is the way to nowhere.
It is not the way to solve the problem.
Simply ignore his post.
|
|
|
| |