SOLUTION: If 104 people attend a concert and tickets for adults cost $2.25 while tickets for children cost $1.75 and total receipts for the concert was $202.5, how many of each went to the c

Algebra ->  Customizable Word Problem Solvers  -> Finance -> SOLUTION: If 104 people attend a concert and tickets for adults cost $2.25 while tickets for children cost $1.75 and total receipts for the concert was $202.5, how many of each went to the c      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1050974: If 104 people attend a concert and tickets for adults cost $2.25 while tickets for children cost $1.75 and total receipts for the concert was $202.5, how many of each went to the concert?
______ Adults
______ Children
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
x how many children
y how many adults
system%28x%2By=104%2C1.75x%2B2.25y=202.5%29

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
If 104 people attend a concert and tickets for adults cost $2.25 while tickets for children cost $1.75
and total receipts for the concert was $202.5, how many of each went to the concert?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Solution 1 (using one equation in one unknown) 

Let x be the number of adult ticket bought.
Then the number of children tickets bought is (104-x).

The "value" equation is

225*x + 175(104-x) = 20250.   (1)

Reduce by 25 all terms in both sides:

9x + 7*(104-x) = 810.

9x + 728 - 7x = 810,

2x = 810 - 728,

2x = 82   --->  x = 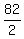82%2F2 = 41.

Answer.  41 adult tickets and 104-41 = 63 children tickets.

Solution 2 (using a system of two equations in two unknown) 

Let "x" be the number of the adult    ticket bought, and
let "y" be the number of the children ticket bought.

Then you have a system of two linear equations in two unknowns

   x +    y = 104,           (1)
225x + 175y = 20250.         (2)  (this is the "value" equation in cents)

From the equation (1), express y = 104-x, and substitute this expression into the equation (2). You will get

225*x + 175(104-x) = 20250.  (3)

The equation (3) is a single equation for the unknown "x".
It coincides with the equation (1) of the Solution 1 above.
Use the same procedure as in the Solution 1 to find "x".
Then find "y".

You will get the same answer, of course.