Question 1049064: The lengths of the sides of a triangle are consecutive even integers. A rectangle whose dimensions are the same as the longer of the two sides of the triangle has a perimeter that is 1.5 times that of the triangle. What are the dimensions of the rectangle?
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39615)   (Show Source): (Show Source):
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The lengths of the sides of a triangle are consecutive even integers. A rectangle whose dimensions are the same as the longer of the two sides of the triangle has a perimeter that is 1.5 times that of the triangle. What are the dimensions of the rectangle?
A triangles DOES NOT have 2 sides. Why would you say this: "A rectangle whose dimensions are the same as the longer of the two sides of
the triangle?" If what you actually mean is that the rectangle's dimensions are the same as the 2 LONGER sides of the triangle, then read on.
Let the smallest side of the triangle be S
Then middle and longest sides are: S + 2, and S + 4, respectively
Therefore, dimensions of rectangle are: S + 2, and S + 4
Perimeter of rectangle: 2(S + 2 + S + 4), or 2(2S + 6), or 4S + 12
Perimeter of triangle: S + S + 2 + S + 4, or 3S + 6
We then get: 4S + 12 = 1.5(3S + 6)
4S + 12 = 4.5S + 9
4S - 4.5S = 9 - 12
- .5S = - 3
S, or smallest side of triangle = 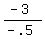 , or 6 units , or 6 units
Dimensions of rectangle:  , and , and 
|
|
|