|
Question 1041797: a man borrowed 120,000 and promised to pay annually for 5 years. the payment start at "x" pesos. the man intends to increase his payments by 5000 at the end of each successive year. if the interest rate is 8% compounded annually, how much will the first payment be?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the man borrows 120,000 pesos.
the interest rate is 8% per year compounded annually.
the present value of all his payments must be equal to 120,000.
since it's not the same payment each year, you will need to look at each year separately.
your payments at the end of each year will be:
end of year 1 = x
end of year 2 = x + 5000
end of year 3 = x + 10000
end of year 4 = x + 15000
end of year 5 = x + 20000
the present value of these payments needs to be equal to 120,000.
the present value of each of these payments will be:
present value of first payment = x / 1.08
present value of second payment = (x + 5000) / 1.08^2
present value of third payment = (x + 10000) / 1.08^3
present value of fourth payment = (x + 15000) / 1.08^4
present value of fifth payment = (x + 20000) / 1.08^5
these can be made equivalent to:
the present value of:
x/1.08 + x/1.08^2 + x/1.08^3 + x/1.08^4 + x/1.08^5 = first part.
plus:
the present value of 5000/1.08^2 + 10000/1.08^3 + 15000/1.08^4 + 20000/1.08^4 = second part.
the sum of the first part and the second part must be equal to 120,000.
the second part can be calculated easily to get:
the present value of the second part = 36862.12824.
since 120,000 = the sum of the first part and the second part, then you get 120,000 = the first part + 36862.12824.
solve for the first part to get:
first part = 120,000 - 36862.12824 = 83137.87176
this means that:
83137.87176 = x/1.08 + x/1.08^2 + x/1.08^3 + x/1.08^4 + x/1.08^5
if we factor out the x, we get:
83137.87176 = x * (1/1.08 + 1/1.08^2 + 1/1.08^3 + 1/1.08^4 + 1/1.08^5)
simplify this to get:
83137.87176 = x * 3.992710037
solve for x to get x = 83137.87167 / 3.992710037 = 20822.41658
the value of x is equal to 20822.41658.
the first payment will be 20822.41658.
the second payment will be 25822.41658.
the third payment will be 30822.41658.
the fourth payment will be 35822.41658.
the fifth payment will be 40822.41658.
the present value of all these payments at 8% per year will be 120,000.
the last payment is 40822.41658.
the first payment is 20822.41658.
if you recognized that:
83137.87176 = x/1.08 + x/1.08^2 + x/1.08^3 + x/1.08^4 + x/1.08^5 is equivalent to a stream of equal payments at an interest rate of .08 per year, then you could have used an annuity calculator to solve for x.
you would have entered:
present value - 83137.87176
future value = 0
interest rate per year = 8%
number of years = 5
payments are made at the end of each period.
the calculator would have told you that the payment is equal to 20822.42.
one such online calculator you can use can be found at this link.
http://arachnoid.com/finance/index.html
my inputs and results from the use of that calculator are shown below:
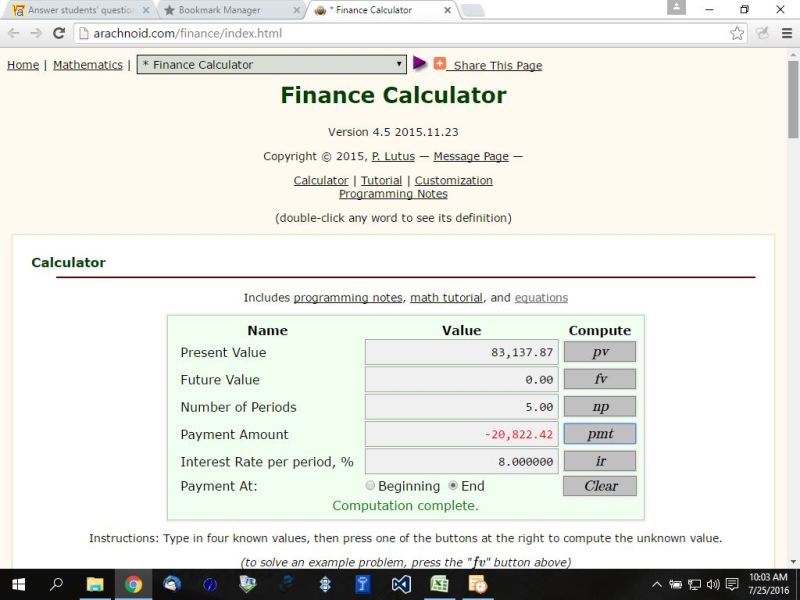
for purposes of this analysis, disregard the sign of the result.
|
|
|
| |