This Lesson (Math circle level problems on finding polynomials with prescribed roots) was created by by ikleyn(52780)   : View Source, ShowAbout ikleyn:
Math circle level problems on finding polynomials with prescribed roots
Problem 1Find the polynomial with roots  , ,  and and  , if , if 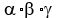 = 6, = 6, 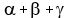 = 5, and = 5, and 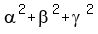 =21. =21.
Solution
We are given
 + +  + +  = 5, (1) = 5, (1)
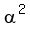 + + 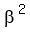 + +  = 21. (2)
It implies = 21. (2)
It implies
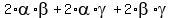 = = 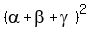 - ( - (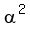 + + 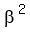 + +  ) = ) =  - -  = 4.
Hence, = 4.
Hence,
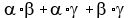 = 2. (3)
Since = 2. (3)
Since  , ,  and and  satisfy equations satisfy equations
 + +  + +  = 5, = 5,
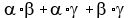 = 2, = 2,
 . . . . = 6,
then by the Vieta's theorem, = 6,
then by the Vieta's theorem,  , ,  and and  are the roots of the cubic equation are the roots of the cubic equation
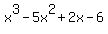 = 0.
Answer. The polynomial with roots = 0.
Answer. The polynomial with roots  , ,  and and  satisfying given conditions is satisfying given conditions is 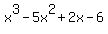 = 0. = 0.
Problem 2Let the roots of the equation x^3 -2x^2 -3x-7=0 be r, s, and t.
Find an equation whose roots are r^2, s^2 and t^2.
Solution
The given equation is
 = 0 (1)
Equation (1) has the roots r, s and t. Therefore, due to to Vieta's theorem
r + s + t = 2, r*s + r*t + s*t = -3, r*s*t = 7. (2)
Now, an equation with the roots = 0 (1)
Equation (1) has the roots r, s and t. Therefore, due to to Vieta's theorem
r + s + t = 2, r*s + r*t + s*t = -3, r*s*t = 7. (2)
Now, an equation with the roots  , , 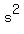 and and  is is
 = 0. (3)
By the Vieta's theorem (or by applying FOIL directly), the coefficients of the left side polynomial are = 0. (3)
By the Vieta's theorem (or by applying FOIL directly), the coefficients of the left side polynomial are
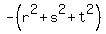 at x^2; (4) at x^2; (4)
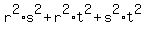 at x; and (5) at x; and (5)
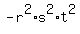 as the constant term. (6)
So, my task now is to express the coefficient (4), (5) and (6) via the coefficients (2) of the equation (1).
Regarding as the constant term. (6)
So, my task now is to express the coefficient (4), (5) and (6) via the coefficients (2) of the equation (1).
Regarding  , it is easy: , it is easy:
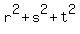 = = 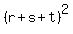 - - 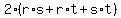 = = 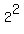 - - 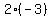 = 4 + 6 = 10.
So, the coefficient at x^2 of the polynomial (3) is = 4 + 6 = 10.
So, the coefficient at x^2 of the polynomial (3) is 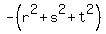 = -10.
Regarding = -10.
Regarding 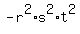 , it is easy, too : , it is easy, too :
 = = 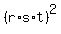 = =  = 49.
So, the constant term of the polynomial (3) is = 49.
So, the constant term of the polynomial (3) is 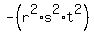 = -49.
Regarding = -49.
Regarding 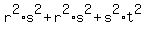 , it is slightly more long way : , it is slightly more long way :
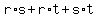 = -3 of (2) implies (squaring both sides)
9 = = -3 of (2) implies (squaring both sides)
9 = 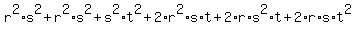 =
= =
= 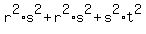 + + 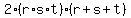 = substituting the known values from (4) =
= = substituting the known values from (4) =
= 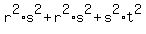 + 2*7*2,
which implies + 2*7*2,
which implies
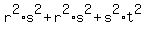 = 9 - 28 = -19.
So, the coefficient at x of the polynomial (3) is = 9 - 28 = -19.
So, the coefficient at x of the polynomial (3) is 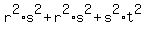 = -11.
Thus we know all three coefficients of the polynomial (3) = -11.
Thus we know all three coefficients of the polynomial (3)
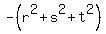 = -10 at x^2; = -10 at x^2;
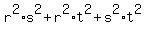 = -19 at x; and = -19 at x; and
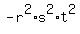 = -49 as the constant term.
Answer. The polynomial equation under the question is = -49 as the constant term.
Answer. The polynomial equation under the question is 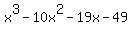 = 0. = 0.
Problem 3The roots of the polynomial equation 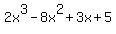 = 0 are = 0 are  , ,  and and  . .
Find the polynomial equation with roots 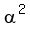 , , 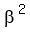 , ,  . .
Solution
The given equation
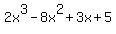 = 0 (1)
is equivalent to = 0 (1)
is equivalent to
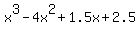 = 0 (2) (all the coefficients of (1) are divided by 2)
Equation (2) has the same roots = 0 (2) (all the coefficients of (1) are divided by 2)
Equation (2) has the same roots  , ,  and and  as equation (1). Therefore, as equation (1). Therefore,
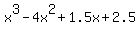 = = 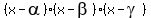 , (3)
and, according to Vieta's theorem , (3)
and, according to Vieta's theorem
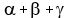 = 4, = 4,  = 1.5, = 1.5, 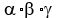 = -2.5. (4)
Now, an equation with the roots = -2.5. (4)
Now, an equation with the roots 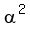 , , 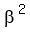 and and  is is
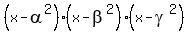 = 0. (5)
By the Vieta's theorem (or by applying FOIL directly), the coefficients of the left side polynomial are = 0. (5)
By the Vieta's theorem (or by applying FOIL directly), the coefficients of the left side polynomial are
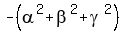 at x^2; (6) at x^2; (6)
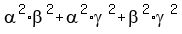 at x; and (7) at x; and (7)
 as the constant term. (8)
So, my task now is to express the coefficient (6), (7) and (8) via the coefficients (4) of the equation (2).
Regarding as the constant term. (8)
So, my task now is to express the coefficient (6), (7) and (8) via the coefficients (4) of the equation (2).
Regarding  , it is easy: , it is easy:
 = =  = = 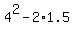 = 16-3 = 13.
So, the coefficient at x^2 of the polynomial (5) is = 16-3 = 13.
So, the coefficient at x^2 of the polynomial (5) is 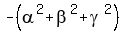 = -13.
Regarding = -13.
Regarding  , it is easy, too : , it is easy, too :
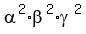 = = 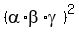 = = 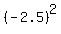 = 6.25.
So, the constant term of the polynomial (5) is = 6.25.
So, the constant term of the polynomial (5) is 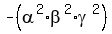 = -6.25.
Regarding = -6.25.
Regarding 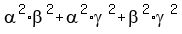 , it is slightly more long way : , it is slightly more long way :
 = 1.5 of (4) implies (squaring both sides)
2.25 = = 1.5 of (4) implies (squaring both sides)
2.25 =  =
= =
= 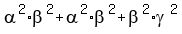 + + 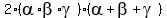 = substituting the known values from (4) =
= = substituting the known values from (4) =
= 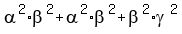 + 2*(-2.5)*4,
which implies + 2*(-2.5)*4,
which implies
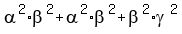 = 2.25 + 20 = 22.25.
Thus we know all three coefficients of the polynomial (5) = 2.25 + 20 = 22.25.
Thus we know all three coefficients of the polynomial (5)
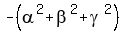 = -13 at x^2; = -13 at x^2;
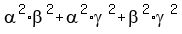 = 22.25 at x; and = 22.25 at x; and
 = -6.25 as the constant term.
Answer. The polynomial equation under the question is = -6.25 as the constant term.
Answer. The polynomial equation under the question is 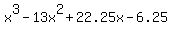 = 0. = 0.
Problem 4Use this identify
tan4Q = 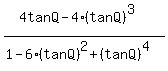
to find the polynomial of least degree that has zeroes 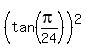 , , 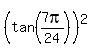 , , 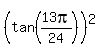 , , 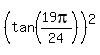 . .
Solution
So, according to the problem formulation, I should accept the given identity "as is", and based on it,
to construct the polynomial.
Since this problem is designed/intendent for advanced students, I will only show the major idea and the major steps
without going in details.
Let me start noticing that of four numbers 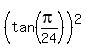 , , 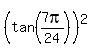 , , 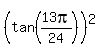 , , 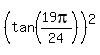 , ,
the first is equal to the third, while the second is equal to the fourth.
So, I will construct the polynomial which has two zeroes as the first and the second numbers of the four numbers listed:
then the third and the fourth numbers will be the roots of this polynomial automatically . . .
Take Q =  . Then 4Q = . Then 4Q =  and tan(4Q) = and tan(4Q) = 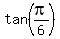 = =  .
According to the given identity, I have then .
According to the given identity, I have then
 = = 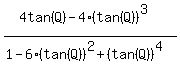 or or
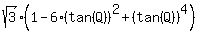 = =  . (2)
Next, in (2), I will replace (tan(Q))^2 by x everywhere (at each appearance).
I will get then . (2)
Next, in (2), I will replace (tan(Q))^2 by x everywhere (at each appearance).
I will get then
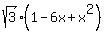 = = 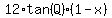 . (3)
Now, for . (3)
Now, for 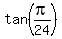 there is the formula (the known expression) there is the formula (the known expression)
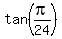 = = 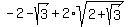 (see the link https://brainly.in/question/9263846 )
and/or (see the link https://brainly.in/question/9263846 )
and/or
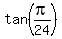 = = 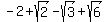 (see the link https://mathworld.wolfram.com/TrigonometryAnglesPi24.html)
Replacing (see the link https://mathworld.wolfram.com/TrigonometryAnglesPi24.html)
Replacing 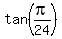 in formula (3) by any of these constant expressions (they are equal (!)),
I get the polynomial of the degree 2 in formula (3) by any of these constant expressions (they are equal (!)),
I get the polynomial of the degree 2
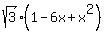 = = 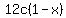 , (4)
whose two roots are , (4)
whose two roots are 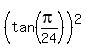 and and 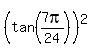 .
Probably, it is more correctly in English to say "a polynomial P(x)", because every product of such a polynomial by a constant
satisfies the problem's conditions, too. .
Probably, it is more correctly in English to say "a polynomial P(x)", because every product of such a polynomial by a constant
satisfies the problem's conditions, too.
My other lessons on Evaluating expressions in this site are
- HOW TO evaluate expressions involving  , , 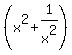 and and 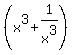
- Advanced lesson on evaluating expressions
- HOW TO evaluate functions of roots of a square equation
- HOW TO evaluate functions of roots of a cubic and quartic equation
- Problems on Vieta's formulas
- Advanced problems on Vieta's theorem
- Miscellaneous problems on Vieta's theorem
- Evaluating expressions that contain infinitely many square roots
- Solving equations that contain infinitely many radicals
- Problems on evaluating in Geometry
- Evaluating trigonometric expressions
- Evaluate the sum of the coefficients of a polynomial
- Miscellaneous evaluating problems
- Advanced evaluating problems
- Lowering a degree method
- Find the number of factorable quadratic polynomials of special form
- Evaluating a function defined by functional equation
- Math circle level problems on evaluating expressions
- Math Olympiad level problem on evaluating a 9-degree polynomial
- Upper league problem on evaluating the sum
- Finding coefficients of decomposition of a rational function
- Upper level problem on evaluating an expression of polynomial roots
- A truly miraculous evaluating problem with a truly miraculous solution
- Entertainment problems on evaluating expressions
- OVERVIEW of lessons on Evaluating expressions
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.
This lesson has been accessed 1542 times.
|

