SOLUTION: Solve the differential equation (x^2 - 8x + 15) dy/dx = 6y + 5

Algebra ->  Customizable Word Problem Solvers  -> Evaluation -> SOLUTION: Solve the differential equation (x^2 - 8x + 15) dy/dx = 6y + 5      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 474425: Solve the differential equation (x^2 - 8x + 15) dy/dx = 6y + 5
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
%28x%5E2+-+8x+%2B+15%29expr%28dy%2Fdx%29+=+6y+%2B+5
Multiply through by dx

%28x%5E2+-+8x+%2B+15%29dy+=+%286y+%2B+5%29dx

Separate the variables:

dy%2F%286y%2B5%29+=+dx%2F%28x%5E2-8x%2B15%29

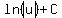
Integrating the left side using formula int%28du%2Fu%29 = ln%28abs%28u%29%29%2BC

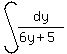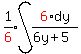int%28dy%2F%286y%2B5%29%29 = expr%281%2Fred%286%29%29int%28red%286%29dy%2F%286y%2B5%29%29 = expr%281%2F6%29ln%286y%2B5%29%2BC%5B1%5D

To integerate the right side, we must first complete the
square on the denominator:

x² - 8x + 15

multiply -8 by 1/2, get -4, then square, getting +16
Add 16 then subtract 16

x² - 8x + 16 - 16 + 15

Factor first three terms as square of a binomian, combine last two terms:

(x - 4)² - 1

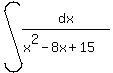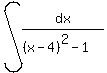int%28dx%2F%28x%5E2-8x%2B15%29%29 = int%28dx%2F%28%28x-4%29%5E2-1%29%29

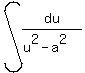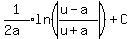
We use formula int%28du%2F%28u%5E2-a%5E2%29%29 = expr%281%2F%282a%29%29ln%28abs%28%28u-a%29%2F%28u%2Ba%29%29%29%2BC

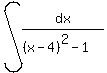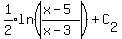int%28dx%2F%28%28x-4%29%5E2-1%29%29 = expr%281%2F%282%2A1%29%29ln%28abs%28%28%28x-4%29-1%29%2F%28%28x-4%29%2B1%29%29%29%2BC%5B2%5D = expr%281%2F2%29ln%28abs%28%28x-5%29%2F%28x-3%29%29%29%2BC%5B2%5D

So we have:

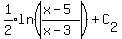expr%281%2F6%29ln%286y%2B5%29%2BC%5B1%5D = expr%281%2F2%29ln%28abs%28%28x-5%29%2F%28x-3%29%29%29%2BC%5B2%5D

Let arbitrary constant C%5B3%5D+=+C%5B2%5D-C%5B1%5D

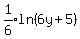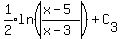expr%281%2F6%29ln%286y%2B5%29 = expr%281%2F2%29ln%28abs%28%28x-5%29%2F%28x-3%29%29%29%2BC%5B3%5D

Multiply through by 6

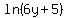ln%286y%2B5%29 = 3ln%28abs%28%28x-5%29%2F%28x-3%29%29%29%2B3C%5B3%5D

Use the coefficient/exponent rule of logarithms and 
write arbitrary constant 3C%5B3%5D as ln%28C%29,
choosing C > 0.

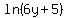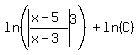ln%286y%2B5%29 = ln%28abs%28%28x-5%29%2F%28x-3%29%29%5E3%29%2Bln%28C%29

Use the sum/product rule of logarithms on the right:

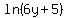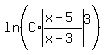
ln%286y%2B5%29 = ln%28C%2Aabs%28%28x-5%29%2F%28x-3%29%29%5E3%29


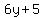6y%2B5 = C%2Aabs%28%28x-5%29%2F%28x-3%29%29%5E3

If the arbitrary constant is chosen properly we may 
erase the absolute values:

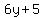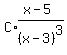6y%2B5 = C%2Aexpr%28%28x-5%29%2F%28x-3%29%5E3%29

or if we like:

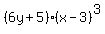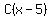%286y%2B5%29%28x-3%29%5E3%29 = C%28x-5%29

Edwin