Question 398690: Ten-digit number. Find a 10-digit number whose first digit
is the number of 1’s in the 10-digit number, whose second
digit is the number of 2’s in the 10-digit number, whose
third digit is the number of 3’s in the 10-digit number, and
so on. The ninth digit must be the number of nines in the
10-digit number and the tenth digit must be the number of
zeros in the 10-digit number
Answer by richard1234(7193)   (Show Source):
You can put this solution on YOUR website! I'll denote the digits  ,  , ...,  . Since there are 1's, 2's, ..., 0's, then  because there are ten digits in the number.
Suppose  . Then a contradiction would result, since there is at least one zero, so  .
Suppose  . Then, this implies that there is exactly one zero within the number, and all the other 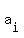 's are at least one, which also creates a contradiction due to the sum of digits. This can also apply to higher values of . If  , then  . Also, if n of the numbers { , , ...,  } are zero, then 9-n of these numbers are greater than or equal to 1, and they sum up to 10-n.
By the Pigeonhole principle, exactly one of the 9-n numbers is equal to 2 and all other nonzero numbers are equal to 1 (this means, 8-n numbers equal to 1). Therefore the number has n zeros, 8-n 1's and one 2. We can easily guess and check based on the value of n, which can only range between 2 and 8. We see that the number 2100010006 satisfies all the given constraints, which happens when  .
|
|
|
