Question 165101: A baseball is hit at a point 3 ft above the ground at a velocity of 100ft/s and at an angle of 45 degrees with respect of the ground. The path of the baseball is given by the function f(x) = -0.0032x2 + x +3 where f(x) is the height of the baseball (in feet) and x is the horizontal distance from home plate (in feet). What's the maximum hieght reached by the baseball?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Remember, the max height occurs at the vertex. So if we find the y-coordinate of the vertex, we find the max height.
Note: the same applies to the min height (if there exists a min height)
In order to find the vertex, we first need to find the x-coordinate of the vertex.
To find the x-coordinate of the vertex, use this formula:  . .
 Start with the given formula. Start with the given formula.
From  , we can see that , we can see that  , ,  , and , and  . .
 Plug in Plug in  and and  . .
 Multiply. Multiply.
 Divide Divide
So the x-coordinate of the vertex is  . .
Now that we know the x-coordinate of the vertex, we can use it to find the y-coordinate of the vertex.
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Square Square 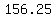 to get to get  . .
 Multiply Multiply
 Combine like terms. Combine like terms.
So the y-coordinate of the vertex is  . .
So the vertex is (156.25,81.125).
Since the y-coordinate is  , this means that the max height is 81.125 ft. , this means that the max height is 81.125 ft.
|
|
|