Question 165093: A 10m by 34m garden is surrounded by a walkway of uniform width (call it "x"). The total area of the garden and walkway is 640 square meters. what is the width of the walkway?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x = width of the path
With these type of problems, it helps to draw a picture. So draw two rectangles, one inside of the other, and label the inside rectangle's dimensions:

Now the label the width of the path "x" (denoted in red)

Since there are 2 "x" lengths per side, this means that you need to add "2x" to both the length and width of the inner rectangle to get the length and width of the outer rectangle. If this makes no sense at all, here's a visual:

So the length and width of the outer rectangle is 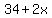 and and  respectively. This means that for the outer rectangle respectively. This means that for the outer rectangle  (the given area of both the walkway and the garden), (the given area of both the walkway and the garden),  and and 
Remember, the area of any rectangle is 
 Start with the area of a rectangle formula Start with the area of a rectangle formula
 Plug in Plug in  , ,  and and 
 FOIL FOIL
 Subtract 640 from both sides. Subtract 640 from both sides.
 Combine like terms. Combine like terms.
Notice we have a quadratic equation in the form of  where where  , ,  , and , and 
Let's use the quadratic formula to solve for x.
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Square Square  to get to get 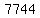 . .
 Multiply Multiply 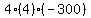 to get to get 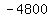
 Rewrite Rewrite 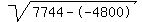 as as 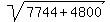
 Add Add 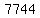 to to  to get to get 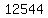
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of 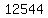 to get to get  . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the possible answers are  or or 
However, since a negative width is not possible, this means that  is NOT a solution. is NOT a solution.
==================================================
Answer:
So the solution is  which means that the width of the path is 3 meters. which means that the width of the path is 3 meters.
|
|
|