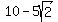SOLUTION: A wire 80 cm in length is cut into two parts and each part is bent to form a square. If the sum of the areas of the squares is 300 cm?, find the lengths of the sides of the two squ

x = length of each side of first square

y = length of each side of second square



We get:



(1)  4x + 4y = 80            <--- from length information  

(2)  x^2 + y^2 = 300         <--- from area information



Eq (1) can be solved for y;  4y = 80-4x ==>  y=20-x



Substitute "20-x" for "y" in (2), to get:

















 From WolframAlpha:





  x = 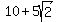 or  x =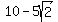 



If x = 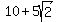, we get  y = 

(which makes sense, it is the other choice for x above, as the assignments of x and y are arbitrary).  



Answer:

  The sides of the two squares measure 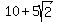 and