|
Question 1202599: Write an exponential model for the following situation. The drug dosage is 375 mg. The drug is eliminated at a rate of 11.3% per hour. Use D=the amount of the drug in milligrams and t=time in hours. Enter your model in the simplified form y=asup(bracket(b),x), and be mindful about the case of your variables.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! the drug dose is 375 milligrams.
the drug is eliminated at a rate of 11.3% per hour.\
D = amount of drug in milligrams.
t = time in hours.
the equation i use most for these if f = p * (1 + r) ^ n
f is the future value
p is the present value
r is the growth rate per time period
(1 + r) is the growth factor per time period.
n is the number of time periods.
in your problem:
p would be equal to 375 milligrams.
r would be -.113 per hour.
(1 + r) would be (1 - .113) = .887 per hour.
n would be the number of hours.
the formula would be simplified to f = 375 * .887 ^ n
replacing f with D and n with t, the formula would becomes D = 375 * .887 ^ t.
this would be you solution to this problem.
if i graph that formula, i would replace D with y and t with x to get y = 375 * .887 ^ x
here's what the graph would look like.
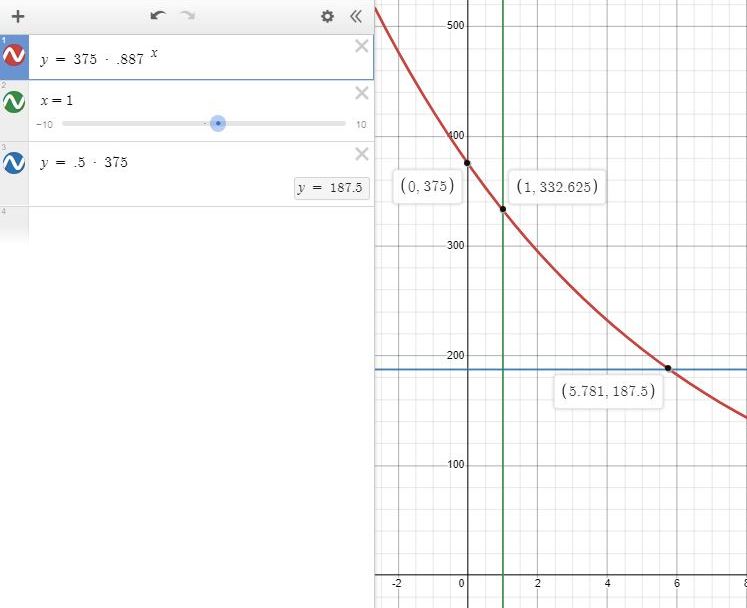
the amount of drug after 1 hours would be D = 375 * .887 ^ 1 = 332.675, as shown in the graph.
the half life of the drug would be calculated as follows:
D = 375 * .887 ^ t becomes 187.5 = 375 * .887 ^ t.
divide both sides of the equation by 187.5 to get .5 = .887 ^ t.
take the log of both sides of the equation to get:
log(.5) = log(.887 ^ t)
by log rule that says log(x^t) equals t * log(x), the formula becomes log(.5) = t * log(.887).
divide both sides of the equation by log(.887) to get log(.5) / log(.887) = t
solve for t to get t = 5.780547624.
round to 3 decimal placdes to get t = 5.781
this agrees with what's on the graph.
don't forget that D is the same as y on the graph and t is the same as x on the graph.
i don't know what y=asup(bracket(b),x), stands for.
a form of the exponential equation would be y = ab^x
if that's the case, then a would be 375 and b would be .887.
y = ab^x would then be y = 375 * .887 ^ x
this is the same as D = 375 * .887 ^ t, with y representing D and x representing t.
let me know if you have any questions.
theo
Answer by ikleyn(52777)  (Show Source):
You can put this solution on YOUR website! .
Write an exponential model for the following situation.
The drug dosage is 375 mg. The drug is eliminated at a rate of 11.3% per hour.
Use D=the amount of the drug in milligrams and t=time in hours.
Enter your model in the simplified form y=asup(bracket(b),x),
and be mindful about the case of your variables.
~~~~~~~~~~~~~~~~~~
Below I present for you a STANDARD mantra on how to solve such problems.
The starting amount of the drug is 375 mg, and the exponential rate of eliminating the drug
is 11.3% per hour. It means that in terms of (D,t) the exponential model is
D = 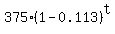 =  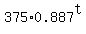. (1)
Here 375 is the initial/starting amount, given in this problem;
1-0.113 = 0.887 is the reducing factor per hour; t is the time, in hours.
+-----------------------------------------------------------------+
| Again, knowing the starting amount and the exponential rate |
| is just ENOUGH to write an exponential model (1) in whole. |
+-----------------------------------------------------------------+
In (y,x) form, formula (1) becomes
y =  .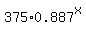
That is all the mantra.
You do not need to pronounce any more words, because excessive words are UNNECESSARY and IRRELEVANT.
Moreover, if you will pronounce excessive words, everybody around will understand immediately
that you do not know the subject and that nobody and never did explain the subject to you in a right way.
-------------------
To see many other similar and different solved problems, look into the lesson
- A medication decay in a human's body
in this site.
|
|
|
| |
