|
Question 1131140: An investor decides to invest some cash in an account paying 12% annual interest, and to put the rest in a stock fund that ends up earning 8% over the course of a year. The investor puts $1000 more in the first account than in the stock fund, and at the end of the year finds the total interest from the two investments was $890. How much money was invested at each of the two rates? Round to the nearest integer.
Answer by ikleyn(52802)   (Show Source):
You can put this solution on YOUR website! .
From the condition, you have this system of 2 equations in 2 unknowns
x = y + 1000, (1) ("The investor puts $1000 more in the first account than in the stock fund")
0.12*x + 0.08*y = 890 (2) (at the end of the year finds the total interest from the two investments was $890.")
where x is the investment at 12% and y is the investment at 8%.
To solve the system, substitute expression (1) into equation (2). You will get
0.12(y+1000) + 0.08y = 890
0.12y + 120 + 0.08y = 890
0.2y = 890 - 120 = 770
y = 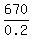 = 3850.
Answer. $3850 invested at 8% and $1000 dollars more, i.e. 4850 dollars invested at 12%.
CHECK. 0.08*3850 + 0.12*4850 = 890 dollars. ! Correct !
Solved.
------------------------
It is a standard and typical problem on investments.
If you need more details, or if you want to see other similar problems solved by different methods, look into the lesson
- Using systems of equations to solve problems on investment
in this site.
You will find there different approaches (using one equation or a system of two equations in two unknowns), as well as
different methods of solution to the equations (Substitution, Elimination).
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|
| |
