Question 989611: Gary has 42 coins in nickels, dimes, and quarters. If he has 8 more nickels than dimes and has $7.15 in all, how many of each does he have?
Found 3 solutions by CubeyThePenguin, josgarithmetic, ikleyn:
Answer by CubeyThePenguin(3113)   (Show Source):
You can put this solution on YOUR website! n = number of nickels
d = number of dimes
q = number of quarters
n + d + q = 42
n = d + 8
5n + 10d + 25q = 715
Substitute the second equation into the first and third equations.
2d + q = 34
15d + 25q = 675
Multiply the first equation by 25.
50d + 25q = 850
-(15d + 25q = 675)
----------------------
35d = 175
d = 5
Gary has 5 dimes, 24 quarters, and 13 nickels.
Answer by josgarithmetic(39620)  (Show Source):
Answer by ikleyn(52814)  (Show Source):
You can put this solution on YOUR website! .
Gary has 42 coins in nickels, dimes, and quarters.
If he has 8 more nickels than dimes and has $7.15 in all, how many of each does he have?
~~~~~~~~~~~
It is a typical problem to be solved using one single unknown and one single equation.
See below on how to do it . . .
Let x be the number of nickels;
then the number od dimes is (x-8) and the number of quarters is (42 - x - (x-8)) = (42+8 - 2x) = (50-2x).
At this point, you can write the total money equation
5x + 10*(x-8) + 25*(50-2x) = 715 cents.
Simplify and solve
5x + 10x - 80 + 1250 - 50x = 715
-35x = 715 + 80 - 1250
-35x = -455
x = 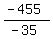 = 13.
ANSWER. 13 nickels; 13-8 = 5 dimes and the rest 42-13-5 = 24 quarters.
CHECK. 13*5 + 5*10 + 25*24 = 715 cents, in total. ! Correct !
Solved.
|
|
|
