Question 934803: A collection of 120 coins worth of $5.52 consists of pennies, nickels, dimes and quarters. There are 8 more nickels than dimes and three times as many pennies as nickels. How many of each type of coin are there?
What I've tried:
x+y+z+w=120
1x+5y+10z+25w=552
y=z+8
x=3y
3y+z+8+z+w=120 1(3y)+5(z+8)+10z+25w=552
3y+2z+w=112 3y+5z+40+10z+25w=552
3y+5z+10z+25w=512
3y+15z+25w=512
(-36y-24z-12w)=-1344
3y+15z+25w=512
(-33y-9z+13w)=-832
Found 3 solutions by TimothyLamb, rothauserc, MathTherapy:
Answer by TimothyLamb(4379)   (Show Source): (Show Source):
You can put this solution on YOUR website! x = pennies
y = nickels
z = dimes
u = quarters
---
x + y + z + u = 120
1x + 5y + 10z + 25u = 552
y = z + 8
x = 3y
---
put the system of linear equations into standard form
---
x + y + z + u = 120
1x + 5y + 10z + 25u = 552
y - z = 8
x - 3y = 0
---
copy and paste the above standard form linear equations in to this solver:
https://sooeet.com/math/system-of-linear-equations-solver.php
---
solution:
x = pennies = 72
y = nickels = 24
z = dimes = 16
u = quarters = 8
---
Free algebra tutoring live chat:
https://sooeet.com/chat.php?gn=algebra
---
Solve and graph linear equations:
https://sooeet.com/math/linear-equation-solver.php
---
Solve quadratic equations with quadratic formula:
https://sooeet.com/math/quadratic-formula-solver.php
---
Solve systems of linear equations up to 6-equations 6-variables:
https://sooeet.com/math/system-of-linear-equations-solver.php
---
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! we have the following formulas
n = d + 8
p = 3n
p = 3*(d+8)
p = 3d+24
d +(d+8) +(3d+24) +q = 120
d+d+8+3d+24+q = 120
5d +32 +q = 120
5d +q = 88
.10d + .05*(d+8) + .01*(3d+24) +.25q = 5.52
.10d +.05d+.4 +.03d+.24 +.25q = 5.52
.18d +.64 +.25q = 5.52
.18d +.25q = 4.88
now we have two equations in two unknowns
5d +q = 88
.18d +.25q = 4.88
solve first equation for q
q = 88 - 5d
substitute for q in second equation
.18d +.25(88-5d) = 4.88
.18d +22-1.25d = 4.88
-1.07d +22 = 4.88
-1.07d = -17.12
d = 16
n = 16+8 = 24
p = 3*24 = 72
q = 120 - (16+24+72) = 8
therefore there are
72 pennies, 24 nickels, 16 dimes, 8 quarters
check answer
.01*72 + .05*24 + .10*16 + .25*8 = 5.52
.72 + 1.20 + 1.60 + 2.00 = 5.52
5.52 = 5.52
our answer checks :-)
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! A collection of 120 coins worth of $5.52 consists of pennies, nickels, dimes and quarters. There are 8 more nickels than dimes and three times as many pennies as nickels. How many of each type of coin are there?
What I've tried:
x+y+z+w=120
1x+5y+10z+25w=552
y=z+8
x=3y
3y+z+8+z+w=120 1(3y)+5(z+8)+10z+25w=552
3y+2z+w=112 3y+5z+40+10z+25w=552
3y+5z+10z+25w=512
3y+15z+25w=512
(-36y-24z-12w)=-1344
3y+15z+25w=512
(-33y-9z+13w)=-832
Due to the fact that it's extremely messy, at times confusing, and doesn't guarantee correct answers,
it's best to avoid creating too many equations with too many variables. Thus, the easiest and best
strategy is to break this down so you only have 2 variables, as follows:
Let number of nickels be N
Then number of dimes is: N - 8, and number of pennies is: 3N
Let number of quarters, be Q
N + N - 8 + 3N + Q = 120 ------ Equation denoting number of each denomination
5N - 8 + Q = 120
5N + Q = 128 ------- eq (i)
.05N + .1(N - 8) + .01(3N) + .25(Q) = 5.52 ------ Equation denoting value of each denomination
.05N + .1N - .8 + .03N + .25Q = 5.52
.18N - .8 + .25Q = 5.52
.18N + .25Q = 6.32 ------- eq (ii)
5N + Q = 128 -------- eq (i)
.18N + .25Q = 6.32 ------- eq (ii)
- 1.25N - .25Q = - 32 ------- Multiplying eq (i) by - .25 ------ eq (iii)
- 1.07N = - 25.68 --- Adding eqs (iii) & (ii)
N, or number of nickels = 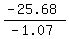 = = 
5(24) + Q = 128 ------- Substituting 24 for N in eq (i)
120 + Q = 128
Q, or number of quarters = 128 120, or 
Number of dimes: 24 8, or 
Number of pennies: 3(24), or 
You can do the check!!
===================
Send comments, thank-yous, and inquiries to D at MathMadEzy@aol.com.
Further help is available, online or in-person, for a fee, obviously.
For FREE info and answers to questions about the ASVAB exam, the NYS 3 8 city/state wide exams,GENERAL
MATH and HOMEWORK QUESTIONS, or MATH QUESTIONS related to the Regents Integrated Algebra,
Regents Geometry, Regents Algebra 2/Trigonometry, SHSAT, COOP/HSPT/TACHS, PSAT, SAT, ACT, SSAT/ISEE,
GRE, CLEP, and the TASC/GED, you can visit: http://asvabstudyzone.freeforums.net/.
|
|
|