Question 720267: I have a mason jar full of coins. Your task is to calculate exactly how many pennies, nickels, dimes and quarters are in the jar. There are 513 coins in the jar. The combined weight of the jar and the coins is 1779 grams. The number of pennies in the jar is twice the sum of the nickels, dimes, and quarters. Quarters weigh 5.8 grams, dimes weigh 2.3 grams, nickels weigh 5.0 grams and pennies weigh 2.5 grams. The jar weighs 301 grams empty.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! calculate exactly how many pennies, nickels, dimes and quarters are in the jar.
There are 513 coins in the jar.
The combined weight of the jar and the coins is 1779 grams.
The number of pennies in the jar is twice the sum of the nickels, dimes, and quarters.
Quarters weigh 5.8 grams, dimes weigh 2.3 grams, nickels weigh 5.0 grams and pennies weigh 2.5 grams.
The jar weighs 301 grams empty.
:
Write an equation for each statement;
"There are 513 coins in the jar.
p + n + d + q = 513
:
"The number of pennies in the jar is twice the sum of the nickels, dimes, and quarters."
p = 2(n+d+q)
divide both sides by 2
.5p = (n+d+q)
then replace n+d+q with .5p
p + .5p = 513
1.5p = 513
p = 513/1.5
p = 342 pennies
:
"The combined weight of the jar and the coins is 1779 grams.
Quarters weigh 5.8 grams, dimes weigh 2.3 grams, nickels weigh 5.0 grams and pennies weigh 2.5 grams. The jar weighs 301 grams empty."
2.5(342) + 5n + 2.3d + 5.8q = 1779 - 301
855 + 5n + 2.3d + 5.8q = 1478
5n + 2.3d + 5.8q = 1478 - 855
5n + 2.3d + 5.8q = 623
and we know
n + d + q = 513 - 342
n + d + q = 171
multiply by 5 and subtract weight equation
5n + 5d + 5q = 855
5n+2.3d+5.8q = 623
-------------------subtracting eliminates n
2.7d - .8q = 232
2.7d = .8q + 232
Divide by 2.7
d =  q + q + 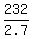
Using the table of this equation on a Ti83, came up with integer values for d and q
d = 96
q = 34
Find n
n + 96 + 34 = 171
n = 171 - 130
n = 41
:
I get 342 pennies, 41 nickels, 96 dimes, 34 quarters
Check this, find the weight of each type of coin plus weight of the jar:
342(2.5) + 41(5) + 96(2.3) + 34(5.8) + 301 = 1779
:
-----------------------
Actually there is another solution to the problem which you can confirm
342 pennies, 76 nickels, 88 dimes, 7 quarters
:
We had to resort to finding integers from the Ti83 equation, because we had 4 unknowns and only 3 equations.
|
|
|