Question 643580: Can you please help me on this question I have tried over and over again to get it right but i get it wrong.
Veronica has pennies, nickels, and dimes in her purse, for a total of 32 coins. If the number of pennies is 3 more than twice the number of nickels, and the number of dimes is 4 less then the number of pennies, how many of each does she have? Thank you for your help!
Jasdeep Kaur
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Veronica has pennies, nickels, and dimes in her purse, for a total of 32 coins.
If the number of pennies is 3 more than twice the number of nickels, and the
number of dimes is 4 less then the number of pennies,
how many of each does she have?
:
let p = no. of pennies
let n = no. of nickels
let d = no. of dimes
:
Write an equation for each statement;
Re-arrange the last two equations get d and n in terms of p:
:
"Veronica has pennies, nickels, & dimes in her purse, for a total of 32 coins."
p + n + d = 32
:
"the number of pennies is 3 more than twice the number of nickels,"
p = 2n + 3
p - 3 = 2n
or
2n = p - 3
divide both sides by 2
n = 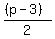
:
"The number of dimes is 4 less then the number of pennies,"
d = p - 4
:
Replace n and d in the 1st equation
p + 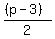 + (p-4) = 32 + (p-4) = 32
2p + 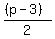 = 32 + 4 = 32 + 4
2p + 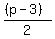 = 36 = 36
Multiply by 2 to get rid of the fraction
2(2P) + (p-3) = 2(36)
4p + p = 72 + 3
5p = 75
p = 75/5
p = 15 pennies
:
Find the nickels
n = 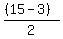
n = 6 nickels
:
find dimes
d = 15 - 4
d = 11 dimes
:
:
See if this adds up: 15 + 6 + 11 = 32
|
|
|