Question 413830: How many ways can 4 nickels and 5 dimes be distributed among 9 children if each is to recieve one coin?
Found 2 solutions by bayners123, richard1234:
Answer by bayners123(12)   (Show Source):
You can put this solution on YOUR website! Interesting question!
To solve you will first have to consider that all of the coins are unique, and then reduce your answer to allow for the fact that they are not the same so some combinations will be the same.
so, if they were all different:
Consider we go and hand one coin to each child in turn. The first child will get one of the 9 coins, the second will then get one of 8 (as they can not get the same one as the first), the third will get one of 7 and so on. This means that the total amount of combinations will be given by
9x8x7x6x5x4x3x2x1
In maths we use an ! to show this, so we can say there are 9! (9 factorial) combinations.
However we need to allow for repeats... This is quite a difficult concept and not easy to explain by text...
Basically though we need to know how many repeats there are of the coins. If only 2 of the coins were the same, the value of 9! would be twice as large as the answer you wanted (as we would have allowed for child one getting one nickel and child two getting the other as one combination, and child two getting the first and child one getting the other for every combination, whereas because these coins are the same, and not distinguishable these combinations are all the same)
So now we dont just have 2 the same, we have 4 the same and 5 the same. So with the 5 this means that for every combination that there actually is, we will have calculated far to many in the 9! value. Again on the similar logic as before there will be 5! times too many values in fact, and with the four coins the same 4! too many.
I have tried to make this clear but realise that it is probably quite uncomprehendable! But basically the formula that you need for this sort of question is:
with as many repeats on the bottom as you have (here only the 2)
In this case this would mean the solution would be 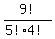 which gives a total of 126.
Hope that helps and wasn't too confusing!
Answer by richard1234(7193)  (Show Source):
You can put this solution on YOUR website! There are 9! ways to distribute one coin to each child, but we have four nickels and five dimes which are assumed to be indistinguishable. To account for overcounting, we divide by 4!5! (because all 4! arrangements of nickels would be counted as one, same with dimes), so the total number is  .
|
|
|
