SOLUTION: Sam has $3.15 in quarters nickels and dimes he has half as many quarters as he has dimes and nickels together he also has two more nickels than dimes how many of each coin are the

Let d be the number of dimes.  

Then the number of nickels "n" is n = (d+2),   according to the condition.

Also, the number of quarters is 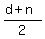 =  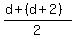=  = d+1,   according to the condition.


Thus dimes contribute  10*d cents to the total.

Nickels contribute      5*(d+2) cents to the total.    (<<<---=== because the number of nickels is (d+2), as it was said above)

Quarters contribute     25*(d+1) cents to the total.   (<<<---=== because the number of quarters is (d+1) as it was shown above)


Then your money equation is

Dimes + Nickels + Quarters = 315   cents,   or

10d   + 5*(d+2) + 25(d+1)  = 315.


Simplify and solve for d:

10d + 5d + 10 + 25d + 25    = 315

40d = 315 - 10 - 25 = 280  ====>  d =  = 7.


Answer.  There were 7 dimes,  d+2 = 7+2 = 9 nickels and  d+1 = 7+1 = 8 quarters. 


Check.   7*10 + 5*9 + 8*25 = 315.    ! Correct !

    This problem is FOR ONE unknown, NOT FOR THREE.

    Therefore your task is carefully choose the leading/the major unknown;

        then express other unknowns via this leading one;

        then to make your equation;

        then carefully solve it.

For a moment, let's place aside two nickels and one quarter.


Then we will have a collection, which is worth  315-2*5-1*25 = 280 cents and has equal number 
of dimes and nickels, while the number of dimes and nickels together is twice the number of quarters.


From it, we logically conclude that in this modified collection, the number of quarters is the same 
as the number of dimes and is the same as the number of nickels.


It means that we can group the coins in the sets in a way that each set contains 
one quarter, one dime and one nickel.


It is easy to compute mentally that each such set is worth 25 + 10 + 5 = 40 cents.

Hence, the number of the sets is 280/40 = 7.


Thus, the modified collection has 7 quarters, 7 dimes and 7 nickels


Now, returning to the original collection, we find that it has 7+1 = 8 quarters, 7 dimes and 7+2 = 9 nickels.

Apparently the younger generation doesn't see any need for punctuation marks or
capital letters to separate sentences.  They just run them all together. And
soon the correct way to write will include "u" for "you", "r" for "are",
"before" as "b4", "8" for "ate", etc.  

In that light, there are plenty of sites online where you only have to type in a
system of equations, point and click, and the answer pops out instantaneously.
So why not use them?   You can even do it on a TI-84 calculator, if you install
the right program.  Why hitch a horse to a buggy and get there in an hour, when
you can drive a car and get there in 10 minutes? 

If you use a separate letter for each unknown, setting up the equations is a
cinch. This system below is set up directly from the words:



Go to one of those sites. Type that in. Point and click, and instantly you 
get q=8, d=7, n=9.  Here is a link to such a site:

https://www.emathhelp.net/en/calculators/algebra-2/system-of-equations-solver/?

Edwin

In fact, you can even use artificial intelligence.  You cannot trust AI for
advanced stuff, but it can solve simple stuff very easily.  I copied and pasted
exactly word-for word what you posted above (without punctuation marks) into: 

https://poe.com/

and here's what I got (copied and pasted) from that site:

-------------------------------------

Let's define the variables for the coins:

Let 𝑑 be the number of dimes.
Let 𝑛 be the number of nickels.
Let 𝑞 be the number of quarters.

From the problem, we have the following relationships:

The total value of the coins is $3.15, which is 315 cents:

10𝑑+5𝑛+25𝑞=315

Sam has half as many quarters as the total number of dimes and nickels:
𝑞=1/2(𝑑+𝑛)

He has two more nickels than dimes:
𝑛=𝑑+2

Now, we can substitute 𝑛 in terms of 𝑑 into the other equations. 

From the third equation, we have: 𝑛=𝑑+2

Substituting 𝑛 into the second equation:
𝑞=(1/2)(𝑑+(𝑑+2))=(1/2)(2d+2)=d+1

Now substituting 𝑛 and 𝑞 into the first equation:

10𝑑+5(𝑑+2)+25(𝑑+1)=315

Expanding this gives:

10𝑑+5𝑑+10+25𝑑+25=315

40𝑑+35=315

Now, subtract 35 from both sides:

40𝑑=280

Dividing by 40:

𝑑=7

Now that we have d, we can find 𝑛 and 𝑞
𝑛=𝑑+2=7+2=9
𝑞=𝑑+1=7+1=8

Thus, the solution is:

Dimes (d): 7
Nickels (𝑛): 9
Quarters (𝑞): 8
Final Answer:

Dimes: 7
Nickels: 9
Quarters: 8

-------------------------

That was all copied and pasted exactly as poe.com printed instantly. But
don't depend on it for more advanced math.  It will sometimes make stupid
mistakes.  AI is not perfected yet.  But someday it will be, and will take us
all over, just as Stephen Hawking warned. LOL (Maybe I shouldn't be laughing).

Edwin

Sam has $3.15 in quarters nickels and dimes he has half as many quarters as he has dimes and nickels together he also has two more nickels than dimes how many of each coin are there

Appears as though this should be written as:
"Sam has $3.15 in quarters, nickels, and dimes. He has half as many quarters as he has dimes and nickels, together. 
 He also has two more nickels than dimes. How many of each coin are there?"

Let number of dimes be D
Then number of nickels is D + 2 (He has 2 more nickels than dimes)
Number of quarters:  (He has half as many quarters
                                                         as he has dimes and nickels, together)
Amount in DIMES: .1D
Amount in NICKELS:  .05(D + 2) = .05D + .1
Amount in QUARTERS: .25(D + 1) = .25D + .25 
Total amount: $3.15 
We then get: .1D + .05D + .1 + .25D + .25 = 3.15
                                .4D + .35 = 3.15
                                      .4D = 2.8
                   Number of dimes, or 

                 Number of nickels: D + 2 = 7 + 2 = 9
                Number of quarters: D + 1 = 7 + 1 = 8