Question 1052972: Harry has $6.10 in his pocket. He has twice as many quarters as nickels and one more dime than quarters. How many of each coin does Harry have
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Harry has $6.10 in his pocket. He has twice as many quarters as nickels and one more dime than quarters.
How many of each coin does Harry have
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
For a moment, take off one dime from the collection (mentally).
Then you can group the remaining coins in the sets (1n, 2d, 2q) containing 1 nickel, 2 dimes and 2 quarters in each set.
The worth of each set is 5+2*10+2*25 = 75 cents.
The number of these groups is 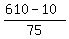 = = 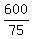 = 8.
Thus there are 8 nickels, 16 dimes, and 16 quarters among remained coins.
So, the answer is: 8 nickels, 16+1 = 17 dimes, and 16 quarters in the original collection. = 8.
Thus there are 8 nickels, 16 dimes, and 16 quarters among remained coins.
So, the answer is: 8 nickels, 16+1 = 17 dimes, and 16 quarters in the original collection.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! Harry has $6.10 in his pocket.
$0.25Q + $0.10D + $0.05N = $6.10
or multiplying through by 100,
25Q + 10D + 5N = 610
dividing through by 5
5Q + 2D + N = 122
He has twice as many quarters as nickels
Q = 2N
and
one more dime than quarters.
D = Q + 1
So we have this system of equations:
1. 5Q + 2D + N = 122
2. Q = 2N
3. D = Q + 1
Use eq. 2 to substitute 2N for Q in eq. 3
3. D = Q + 1
4. D = 2N + 1
Use eq. 2 to substitute 2N for Q in eq. 1 and
use eq. 4 to substitute 2N + 1 for D in eq 1:
1. 5Q + 2D + N = 122
5(2N) + 2(2N + 1) + N = 122
10N + 4N + 2 + N = 122
15N + 2 = 122
15N = 120
N = 8
Substitute 8 for N in eq. 4:
4. D = 2N + 1
D = 2(8) + 1
D = 16 + 1
D = 17
Substitute N=8 in eq. 2
2. Q = 2N
Q = 2(8)
Q = 16
Edwin
|
|
|