Question 894462: 1.If the DOB of Grand son and Grand Father is same and for six consecutive years Grand Father's age in multiple of Grand Son's age what will be the age of Grand Son and Grand Father?
2.Prove that Root3+7 is irrational number
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. A grandfather and grandson celebrate their birthdays on the same day of the year, and for 6 consecutive years the grandfather's age is a multiple of the grandson's age.
SOLUTION:
on the first of those 6 consecutive years the grandfather is 61, and the grandson is 1,
on the second year, their ages are 62 and 2;
on the third year, their ages are 63 and 3;
on the fourth year, their ages are 64 and 4;
on the fifth year, their ages are 65 and 5, and
on the sixth year, the grandfather is 66, and the grandson is 6.
REASONING:
Starting with a very young grandson makes sense, so we start with a 1 year old grandson, who will be 2, 3, 4, 5, and 6 in the next 5 consecutive years.
If the grandfather's age on the first year is  , ,
it is a multiple of the grandson's age, which is  , ,
but in the next 5 years it must be that
 is a multiple of 2; is a multiple of 2;
 is a multiple of 3; is a multiple of 3;
 is a multiple of 4; is a multiple of 4;
 is a multiple of 5, and is a multiple of 5, and
 is a multiple of 6. is a multiple of 6.
That weans that  is a multiple of 2, 3, 4, 5, and 6. is a multiple of 2, 3, 4, 5, and 6.
The least common multiple of those numbers is  . .
 ---> --->  gives the grandfather a reasonable age. gives the grandfather a reasonable age.
COMMENT:
Other common multiples of 2, 3, 4, 5, and 6, like 120, 180, and so on, make the grandfather way too old.
As another unrealistic option, we could start with a grandson who is 2 and a grandfather whose age minus 2 is a multiple of 2, 3, 4, 5, 6 and 7. Since the least common multiple is 210, that would make the grandfather at least 212. Making the grandson even older, makes the grandfather even more ridiculously old.
2. 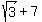 is irrational, because is irrational, because  is irrational. is irrational.
If 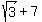 were rational, were rational,  , being the sum of two rational numbers would be rational. , being the sum of two rational numbers would be rational.
The fact that  is irrational is proven like the fact that is irrational is proven like the fact that  is irrational. is irrational.
If  were rational, it could be written as an irreducible fraction, were rational, it could be written as an irreducible fraction,
 with with  and and  not having any common factors. not having any common factors.
Then,
 ---> --->  ---> --->  ---> --->  . .
That means that 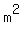 is a multiple of 3, is a multiple of 3,
but then  must be a multiple of 3, must be a multiple of 3,
which would make 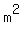 a multiple of 9, and a multiple of 9, and  would be a multiple of 3, just like would be a multiple of 3, just like  is. is.
That contradicts the starting hypothesis that  with with  and and  not having any common factors. not having any common factors.
So, it is impossible to find a rational number 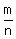 with with  and and  not having any common factors, and not having any common factors, and  . .
In other words, it is impossible to find a rational number equal to  , so , so  is irrational. is irrational.
|
|
|