Question 697110: A father says to his son that at the time of his birth he was 3 times older than him. If now father's present age is 18 years, then what was the age of son 4 years ago?
ANS: 8 years. But how?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There has to be a typo. A father that young sound unreasonable, and the math results in ages that are not integers.
WHAT SHOULD HAVE BEEN:
The father's present age is  years. years.
That can be solved as follows:
 = age of the son 4 years ago = age of the son 4 years ago
 = age of the son now. = age of the son now.
The equation can be set up all at one as

Going slower, to show the rationale:
The son's current age is  years. years.
The father says "I was 3 times as old as that when my son was born."
That means that the father was  when his son was born. when his son was born.
Since that was  years ago, years ago,
now the father must be 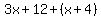 years old. years old.
 and that equals and that equals  , so , so
 --> -->  --> -->  --> -->  --> --> 
THE PROBLEM AS POSTED
 = age of the son 4 years ago = age of the son 4 years ago
 = age of the son now = age of the son now
The equation that results is

It simplifies as before
 --> -->  --> -->  --> -->
It solves as before
 --> -->  --> -->  --> --> 
That would make the son 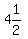 years old now. years old now.
But it does not make sense to say that the son was  year old four years ago (we would say he was just 6 months old) year old four years ago (we would say he was just 6 months old)
While the son may proudly be saying "I am four and a half years old now,"
I would call that being just 4 years old, because age is usually stated as the age at the latest birthday, without fractions.
Furthermore, the father saying "I was 3 times as old when you were born" could mean
 years old, or years old, or
 years old (if we accept fractional ages), years old (if we accept fractional ages),
and either way that would be too young.
|
|
|