Question 696107: A guy is her mom's age with digits reversed (e.g. 34 and 43). A year ago he was half her mom's age. How old are they now?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! THE ALGEBRA WAY TO SOLVE IT:
Setting up:
 = first (tens) digit of that guy's age. = first (tens) digit of that guy's age.
 = second (ones) digit of that guy's age. = second (ones) digit of that guy's age.
The guy's age is  . .
His mother's age is 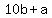 . .
Last year, the guy was 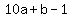
and his mother was 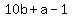 , ,
which was twice the guy's age, so

Solving:
 --> -->  --> -->  --> --> 
At this point we could start trying values for  , ,
knowing that it is a small odd number.
It must be odd to make 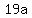 equal to the obviously odd equal to the obviously odd 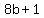 . .
It is small because it is the first digit of the son's age,
and the mother's is more than twice that, but no more than 99.
Otherwise,  <--> <--> 
We see that  must be a multiple of 8 plus 1. must be a multiple of 8 plus 1.

At this point, we should see  with with  as an obvious answer. as an obvious answer.
(Otherwise, we could try  values starting with values starting with  to find that only to find that only  works, works,
because  and and  would yield fractional values for would yield fractional values for  , ,
and  would yield would yield  ). ).
Substituting into  , we get , we get
 --> -->  --> -->  --> -->  --> -->  --> --> 
The guy is  and his mom is and his mom is  . .
|
|
|