SOLUTION: Prove that in a group of ten persons there are at least two such that either the sum or the difference of their ages is divisible by 16. Do not prove by example. Cover all cases.

Algebra ->  Customizable Word Problem Solvers  -> Age -> SOLUTION: Prove that in a group of ten persons there are at least two such that either the sum or the difference of their ages is divisible by 16. Do not prove by example. Cover all cases.      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 694982: Prove that in a group of ten persons there are at least two such that either the sum or the difference of their ages is divisible by 16. Do not prove by example. Cover all cases.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I believe that for the purposes of this problem the number zero is supposed to be considered divisible by 16. Otherwise, for a group of ten 1-year olds, there would not be two of them such that either the sum or the difference of their ages is divisible by 16. (The sum would always be 2, and the difference would always be 0).

Dividing by 16 the age of each person in the group there would be an integer quotient and integer remainder, r, such that 0%3C=r%3C=15.

If two people in the group have the same r, the difference of their ages is a multiple of 16 or zero.
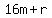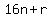The ages would be 16m%2Br and 16n%2Br (m and n would be the quotients obtained when dividing their ages by 16).
The difference of ages would be
abs%2816m%2Br-%2816n%2Br%29%29=abs%2816m%2Br-16n-r%29=abs%2816%28m-n%29%29=16abs%28m-n%29 and that is either a multiple of 16, or zero, considered to be divisible by 16 in either case.

If no two people in the group have the same 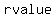r+value, the differences of ages will not be divisible by 16, but what happens with the sum of their ages?
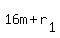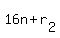The ages would be 16m%2Br%5B1%5D and 16n%2Br%5B2%5D, and their sum would be
16m%2Br%5B1%5D%2B16n%2Br%5B2%5D=16%28m%2Bn%29%2B%28r%5B1%5D%2Br%5B2%5D%29
If the r values add up to 16, the sum of the ages would be
16%28m%2Bn%29%2B16=16%28m%2Bn%2B1%29, divisible by 16.
at least two of them will have r values that add to 16.

In a group of 10 people, there are at least two whose r values add up to 16, because except for r=0 and r=8, the other (14) possible r values can be paired up so that each of those (7) pairs add to 16:
1%2B15=16
2%2B14=16
3%2B13=16
4%2B12=16
5%2B11=16
6%2B10=16
7%2B9=16
In a group of people you could have 9 such that the sum of the r values of any pair of them is not 16. The r's would be 0, 8, and one member of each of the pairs listed above. The 10th different r would be part of one of the 7 pairs, adding up to 16 with one of the 9 previous r values.

This can be called a problem of modular arithmetic, and there is probably a more succinct and elegant proof. The people at the forums in artofproblemsolving.com would love such problems and would solve them, but they may not explain much, and they may use jargon that you are not used to. However, they may be worth a try.