Question 613761: Mr. Gibbs has 3 sons: Joe, John, and Mark. The sums of their ages is equal to the age of their Father. In 1 year, Mr. Gibbs will be twice as old as Joe. In 2 years, Mr. Gibbs will be 3 times as old as John. In 3 years, Mr. Gibbs will be four times as old as Mark. How old is each son now?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Mr. Gibbs has 3 sons: Joe, John, and Mark. The sums of their ages is equal to the age of their Father.
In 1 year, Mr. Gibbs will be twice as old as Joe. In 2 years, Mr. Gibbs will be 3 times as old as John.
In 3 years, Mr. Gibbs will be four times as old as Mark. How old is each son now?
:
let j = Joe's age
let n = John's age
let m = Mark's age
Let g = father's age
:
Write an equation for each statement
:
Mr. Gibbs has 3 sons: Joe, John, and Mark. The sums of their ages is equal to the age of their Father.
j + n + m = g
:
In 1 year, Mr. Gibbs will be twice as old as Joe.
2(j+1) = g + 1
2j + 2 = g + 1
2j = g + 1 -2
2j = g - 1
j = 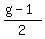
:
In 2 years, Mr. Gibbs will be 3 times as old as John.
3(n+2) = g + 2
3n + 6 = g + 2
3n = g + 2 - 6
3n = g - 4
n = 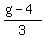
:
In 3 years, Mr. Gibbs will be four times as old as Mark.
4(m+3) = g + 3
4m + 12 = g + 3
4m = g + 3 - 12
4m = g - 9
m = 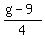
:
How old is each son now?
:
replace j, n, m
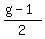 + + 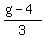 + + 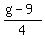 = g = g
multiply by 12, to get rid of the denominators, results
6(g-1) + 4(g-4) + 3(g-9) = 12g
6g - 6 + 4g - 16 + 3g - 27 = 12g
Combine like terms
6g + 4g + 3g - 6 - 16 - 27 = 12g
13g - 49 = 12g
13g - 12g = 49
g = 49 yrs is Dad's age
:
Find j
j = 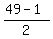
j = 24 yrs is Joe's age
Find n
n = 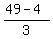
n = 15 yrs is John's age
Find m
m = 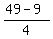
m = 10 yrs is Mark's age
;
:
see if that works out,
"The sums of their ages is equal to the age of their Father"
24 + 15 + 10 = 49
|
|
|