In 1996 my grandfather's age equaled the product of the four digits in the year he was born and the same was true for his daughter. Find the two birth years.
We know all the years start with 19. Let's just consider the
last two digits of the year. For example 1996 will be called just
96 and, say, 1935 would, for instance, be called just 35.
96 - age = birth year
let t = tens digit of the birth year
let u = units digit of the birth year
birth year = 10t + u
1·9·t·u = 9tu = product of digits of birth year = age
96 - 9tu = 10t + u
Solve for u
96 - 10t = 9tu + u
96 - 10t = u(9t + 1)
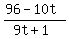 = u
u =
= u
u = 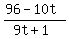 We start trying digits for t until we get a digit for u
try t = 0, u =
We start trying digits for t until we get a digit for u
try t = 0, u = 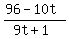 =
=  =
= 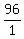 = 96, not a digit
try t = 1, u =
= 96, not a digit
try t = 1, u = 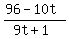 =
= 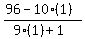 =
=  , not a digit
try t = 2, u =
, not a digit
try t = 2, u = 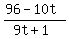 =
= 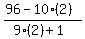 =
= 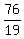 = 4. Hooray, that's a digit, so we found one answer:
t = 2, u = 4, birth year = 1924, age = 1·9·2·4 = 72, must be the grandfather.
Checking 1996-1924 = 72, so that checks.
We need another solution for the daughter:
try t = 3, u =
= 4. Hooray, that's a digit, so we found one answer:
t = 2, u = 4, birth year = 1924, age = 1·9·2·4 = 72, must be the grandfather.
Checking 1996-1924 = 72, so that checks.
We need another solution for the daughter:
try t = 3, u = 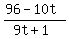 =
= 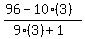 =
= 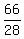 , not a digit.
try t = 4, u =
, not a digit.
try t = 4, u = 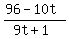 =
= 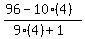 =
= 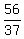 , not a digit.
try t = 5, u =
, not a digit.
try t = 5, u = 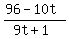 =
=  =
= 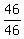 = 1, hooray, another digit.
t = 5, u = 1, birth year = 1951, age = 1·9·5·1 = 45, must be the daughter.
Checking 1996-1951 = 45, so that checks.
Answer: the grandfather was born in 1924 and was 72 in 1996
the daughter was born in 1951 and was 45 in 1996.
Edwin
= 1, hooray, another digit.
t = 5, u = 1, birth year = 1951, age = 1·9·5·1 = 45, must be the daughter.
Checking 1996-1951 = 45, so that checks.
Answer: the grandfather was born in 1924 and was 72 in 1996
the daughter was born in 1951 and was 45 in 1996.
Edwin