Question 333422: For the problem I have to solve it says I have to write a system of equations involving two equations in two variables then to solve the system. Here is the problem: Jean is twice as old as Michael. The sum of their ages 3 years ago was 45 years. Find their ages now.
I tried to solve it without the sytem of equations and i got the answer of jean:32 and Michael:16 but then I realized I would get the question wrong if I didn't show the system of equations. Please help me.
Found 2 solutions by ankor@dixie-net.com, jrfrunner:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here it is step-by-step, it's not that hard.
:
Let j = Jean's present age
let m = Michael's present age
;
Write an equation for each statement
:
"Jean is twice as old as Michael."
j = 2m
:
"The sum of their ages 3 years ago was 45 years."
(j-3) + (m-3) = 45
Simplify
j + m - 6 = 45
j + m = 45 + 6
j + m = 51
:
From the 1st statement equation, replace j with 2m
2m + m = 51
3m = 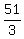
m = 17 yrs is Michael's present age
then we know j = 2m, therefore
j = 2(17)
j = 34 yrs is Jean's present age
:
:
Prove this using the 2nd statment
"The sum of their ages 3 years ago was 45 years."
(34-3) + (17-3) =
31 + 14 = 45
;
Did this make sense to you?
Answer by jrfrunner(365)   (Show Source): (Show Source):
You can put this solution on YOUR website! first, your answers, of Jean=32 and Michael 16, have you tested them to see if they are correct? The sum of their ages 3 years ago was 45 years
Let see, 3 years ago Jean=32-3=29, Michael=16-3=13 so their sum is 42, so your answers are incorrect!
---
Begin by letting J=Jean's age and M=Michaels age, you have two unknowns J and M
and you need as many equations as unknowns.
--
Jean is twice as old as Michael
J=2*M [ this is your first equation ]
---
The sum of their ages 3 years ago was 45 years
J-3 is jean's age 3 years ago
M-3 is Michaels age 3 years ago, so....
(J-3) + (M-3)=45 [ this is your second equation]
---
simplify the second equation
(J-3) + (M-3)=45
J+M-6=45
J+M=51
---
So now you have two equations and 2 unknowns
There are many ways to solve this, substittution, elimination, matrices, graphing, guessing, cramer method, etc......
---
Try subtitution since the first equation is already set to one of the variables
J =2*M
substitute this into the second equation
J+M=51
(2*M)+M=51
3*M=51
M=51/3=17
---
So if M=17 and J=2*M then J=2*(17) =34
====
Check your answers
go back to the original equations
J=2M and (J-3) + (M-3)=45 to see if M=17 and J=34 are valid
|
|
|