Question 167013: The sum of the ages of four daughters, Abigail, Bonnie, Cena, and Daphne, is 40. The difference between the ages of the youngest, Daphne, and the oldest, Abigail, is 6. The second born, Bonnie, is 2 years younger than the oldest, Abigail, and the third born, Cena, is the average of the ages of the youngest, Daphne, and the second born, Bonnie. How old is the father, who is 30 years older than the youngest daughter?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Write an equation for each statement, we will try to get everything in terms of a
:
The sum of the ages of four daughters, Abigail, Bonnie, Cena, and Daphne, is 40.
a + b + c + d = 40
:
The difference between the ages of the youngest, Daphne, and the oldest, Abigail, is 6.
a - d = 6
-d = 6 - a
d = a - 6; multiplied equation by -1
:
The second born, Bonnie, is 2 years younger than the oldest, Abigail,
a - b = 2
-b = 2 - a
b = a - 2
:
third born, Cena, is the average of the ages of the youngest, Daphne, and the second born, Bonnie.
c = 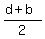
Substitute (a-2) for b and (a-6) for d
c = 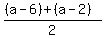 = = 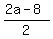
Cancel out the denominator and we have:
c = a - 4
:
Substitute for b, c, d in the first equation, find a:
a + (a-2) + (a-4) + (a-6) = 40
4a - 12 = 40
4a = 40 + 12
4a = 52
a = 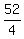
a = 13 yrs is Abigail's age
Then
b = 13 - 2
b = 11 yrs is Bonnie
and
c = 13 - 4
c = 9 yrs is Cena
and
d = 13 - 6
d = 7 yrs is Daphne
:
How old is the father, who is 30 years older than the youngest daughter?
Father = 7 + 30 = 37 yrs old
:
:
Check solution, find the total
13 + 11 + 9 + 7 = 40
:
A lot of steps but not that hard, right?
|
|
|