Question 1202331: Ten years ago Linda was three times christys age then. Ten years from now christys age will be 4/7 of Linda’s age then. How old are they now.
Found 4 solutions by mananth, ikleyn, Edwin McCravy, MathTherapy:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website! Ten years ago Linda was three times christys age then. Ten years from now christys age will be 4/7 of Linda’s age then. How old are they now.
let christy's age 10 years ago be x
Linda's age was 3x
Ten years hence
Christy will be x+20 years
Linda'sage will be 3x +20
x+20 = 4/7 *3x
7(x+20) = 12x
7x+140 = 12x
5x = 140
x = 28 ( christy's age 10 years ago)
So Christy is 28 + 10 = 38 years
Plug x=28
Linda is 3x+10 = 84+20 =94 years
Answer by ikleyn(52798)  (Show Source):
You can put this solution on YOUR website! .
Ten years ago Linda was three times Christy's age then. Ten years from now
Christy's age will be 4/7 of Linda’s age then. How old are they now.
~~~~~~~~~~~~~~~~~~~~
I read, interpret and solve the problem in different way;
so my numbers are different from that of @mananth.
Let x years be the Christy's age 10 years ago;
then Linda's age at that time was 3x years.
Ten years from now Christy's age will be (x+20) years;
Linda's age will be (3x+20) years then.
So, I write equation as the problem states
x + 20 =  .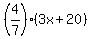
Simplify and find x
7x + 140 = 12x + 80
140 - 80 = 12x - 7x
60 = 5x
x = 60/5 = 12.
ANSWER. Christy's age now is 12+10 = 22 years. Linda's age now is 3*12+10 = 46 years.
CHECK. You may check it on your own that the condition of the problem
"in ten years" is satisfied.
Solved.
Answer by Edwin McCravy(20059)  (Show Source):
You can put this solution on YOUR website!
I would set it up this way. This translates it literally just as it's stated.
The answer comes out same as Ikleyn's. L = 46, C = 22
Edwin
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Ten years ago Linda was three times christys age then. Ten years from now christys age will be 4/7 of Linda’s age then. How old are they now.
This is as clear as "daylight," so I don't know how 1 of these people didn't get it. It's not
surprising though, considering the vast number of wrong answers he/she has been known to produce.
Let Christy's and Linda's ages, be C and L, respectively
Then 10 years ago, Christy was C - 10, while Linda was L - 10
We then get their AGE equation, 10 years ago as L - 10 = 3(C - 10)____L - 10 = 3C - 30___L = 3C - 20 ----- eq (i)
In 10 years' time, Christy will be C + 10, while Linda will be L + 10
We then get their AGE equation, 10 years from now, as 
7C + 70 = 4(L + 10) ------ Multiplying by LCD, 7
7C + 70 = 4L + 40
7C - 4L = - 30 ------ eq (ii)
7C - 4(3C - 20) = - 30 ----- Substituting 3C - 20 for L in eq (ii)
7C - 12C + 80 = - 30
- 5C = - 110'
Christy's age, or 
Knowing Christy's age, you can now find Linda's age using eq (i)!
|
|
|
