Question 1196609: Mark is four years older than Jose, the sum of the squares of their ages is 520 how old is each
Found 3 solutions by josgarithmetic, ikleyn, greenestamps:
Answer by josgarithmetic(39620)   (Show Source):
Answer by ikleyn(52800)  (Show Source):
You can put this solution on YOUR website! .
Mark is four years older than Jose, the sum of the squares of their ages is 520 how old is each
~~~~~~~~~~~~~~~~~
Let x be the number exactly half-way between their ages (x = the arithmetic mean).
Then the older boy is (x+2 ) years old; the younger boy is (x-2) years old.
(x+2)^2 + (x-2)^2 = 520
(x^2 + 2x + 4) + (x^2 - 2x + 4) = 520
Combine like terms
2x^2 + 8 = 520
2x^2 = 520 - 8 = 512
x^2 = 512/2 = 256
x = 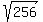 = 16.
ANSWER. Their ages are 16-2 = 14 (younger) and 16+2 = 18 (older).
Solved MENTALLY (without using quadratic equations)
and with full explanations.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
For a purely mental solution, you can reason that, since the two ages are close together, the squares of the ages are relatively close together.
So divide the sum of the squares of their ages, 520, by 2 to get 260, then observe that a perfect square close to 260 is 16^2 = 256; so very likely the two ages (since they are 4 apart) are 16+2=18 and 16-2=14.
Check to see if that works....
18^2+14^2 = 324+196 = 520
ANSWERS: 14 and 18
|
|
|
