SOLUTION: 5 years ago, Fred was one-third Joe’s age. In 10 years, he will be two-thirds of Joe’s age. What is Fred’s age now?

Algebra ->  Customizable Word Problem Solvers  -> Age -> SOLUTION: 5 years ago, Fred was one-third Joe’s age. In 10 years, he will be two-thirds of Joe’s age. What is Fred’s age now?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1188408: 5 years ago, Fred was one-third Joe’s age. In 10 years, he will be two-thirds of Joe’s age. What is Fred’s age now?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

let Fred’s age be F and Joe’s age J
if 5 years ago, Fred was one-third+Joe’s age, we have

F-5=J%2F3
3F-15=J .......eq.1
if in 10 years, Fred will be two-thirds of Joe’s age, we have
F%2B10=2J%2F3
3F%2B30=2J
3F%2F2%2B30%2F2=J
3F%2F2%2B15=J.........eq.2
from eq.1 and eq.2 we have
3F-15=3F%2F2%2B15
3F-3F%2F2=15%2B15
6F%2F2-3F%2F2=30
3F%2F2=30
3F=30%2A2
3F=60
F=60%2F3
highlight%28F=20%29->answer: Fred is 20 years old now
3%2A20-15=J .......eq.1
60-15=J
J=45 ->Joe’s age now

Answer by ikleyn(52800) About Me  (Show Source):
You can put this solution on YOUR website!
.
5 years ago, Fred was one-third Joe’s age.
In 10 years, he will be two-thirds of Joe’s age.
What is Fred’s age now?
~~~~~~~~~~~~~~~


            I read, understand and interpret the problem differently from the other tutor,
            so my solution and my answer are different. 


Let Ferd's age be F and Jow's age be J.


First equation is 

    F - 5 = 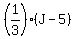%281%2F3%29%2A%28J-5%29


I simplify it to

    3F - 15 = J - 5

    3F -  J = 10.      (1)



Second equation is

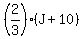    F + 10 = %282%2F3%29%2A%28J%2B10%29.


I simplify it to

    3F + 30 = 2J + 20

    3F - 2J = -10.     (2)


So, I have now this system of two equations in two unknowns

    3F -  J =  10      (1)

    3F - 2J = - 10     (2)


To solve it, apply the Eliminatiom method: from equation (1) subtract equation (2). You will get then

    -J - (-2J) = 10 - (-10)

       J       = 20.


Then from equation (1),  3F - 20 = 10,   3F = 10 + 20 = 30,  F = 30/3 = 10.


ANSWER.  Fred's age is 10 years;  Joe's age is 20 years.


CHECK.   5 years ago, they there 5 and 15 years old.
            
         In 10 years, their ages will be 20 and 30 years,

         so, the problem's conditions are satisfied.

Solved.