Question 1183712: 5 years back the ratio of kate and sharon 4:3. In 5 years, the sum of the ages of kate and sharon will be 90. how old is sharon right now?
Found 3 solutions by josgarithmetic, greenestamps, ikleyn:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If in 5 years the sum of their ages will be 90, then 5 years ago the sum of their ages was 70.
5 years ago the ratio of their ages was 4:3, so let their ages then be 4x and 3x. Then
4x+3x=70
7x=70
x=10
Their ages 5 years ago were 4x=40 and 3x=30.
ANSWER: Sharon's age now is 30+5=35.
-------------------------------------------------------
(Corrected note....)
Note the  METHOD for setting up the problem shown by the other tutor is fine -- although a bit of explanation of HOW to set up that equation would be helpful to a beginning student. Indeed, if they had bothered to try to solve the equation they show, they would have found that the equation was wrong.... METHOD for setting up the problem shown by the other tutor is fine -- although a bit of explanation of HOW to set up that equation would be helpful to a beginning student. Indeed, if they had bothered to try to solve the equation they show, they would have found that the equation was wrong....
If you are going to use a formal algebraic solution, take the time to clearly define your variables and expressions, before writing an equation -- as tutor @ikleyn shows in her response. Trying to write the equation without having a clear understanding of the expressions in the equation can easily lead to errors, as the response from the first tutor shows.
The difference between the setups for the two solutions is that the other tutor's method uses x for Sharon's age now. That has the small advantage of having the answer for "x" being the answer to the problem. But the resulting algebra is more complicated than what is needed for my solution above.
Nearly always, if a problem gives part of the given information in the form of a ratio, the algebra is easier if you use that given ratio directly to set up the problem. In this problem, the "algebra" involved when the problem is set up that way is so basic that it is possible to solve the problem quickly mentally.
It does have the small disadvantage that you have to add 5 to Sharon's age 5 years ago to get her current age....
Answer by ikleyn(52802)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
5 years back the ratio of kate and sharon 4:3.
In 5 years, the sum of the ages of Kate and Sharon will be 90.
How old is Sharon right now?
~~~~~~~~~~~~~~~
In his post, @josgarithmetic writes equation
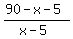 = =  and states that it can be easily solved.
I tried to follow his instruction
3*(90-x-5) = 4*(x-5)
270 - 3x - 15 = 4x - 20
270 - 15 + 20 = 4x + 3x
275 = 7x
x =
and states that it can be easily solved.
I tried to follow his instruction
3*(90-x-5) = 4*(x-5)
270 - 3x - 15 = 4x - 20
270 - 15 + 20 = 4x + 3x
275 = 7x
x = 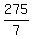 = 39 = 39  .
Notice that this value even is not integer.
@josgarithmetic does not declare what his unknown " x " is.
But it is clear that NEITHER Kate age NOR Sharon age is non-integer number in this problem.
+------------------------------------------------------------------------------------------+
| You may ask: WHAT IS THE MATTER ? |
| |
| |
| The matter is that this @josgarithmetic's setup equation is I N C O R R E C T. |
| | |
| In other words (to make my statement even more clear), it is W R O N G. |
+------------------------------------------------------------------------------------------+
Unfortunately, tutor @greenestamps MISSED this error and declared the @josgarithmetic's setup as "fine", instead.
THEREFORE, I came to prevent this huge mistake considering the WRONG setup as a correct.
+-------------------------------------------+
| The correct setup would be AS FOLLOWS |
+-------------------------------------------+
Let x be the Sharon present age.
Then 5 years ago Sharon's age was (x-5) years.
The Kate's age in 5 years will be 90 - (x+5);
hence, the Kate's age 5 years back was (90 - (x+5) - 10) = 80-(x+5) years.
Now we can write equation describing the ratio of their ages 5 years back .
Notice that this value even is not integer.
@josgarithmetic does not declare what his unknown " x " is.
But it is clear that NEITHER Kate age NOR Sharon age is non-integer number in this problem.
+------------------------------------------------------------------------------------------+
| You may ask: WHAT IS THE MATTER ? |
| |
| |
| The matter is that this @josgarithmetic's setup equation is I N C O R R E C T. |
| | |
| In other words (to make my statement even more clear), it is W R O N G. |
+------------------------------------------------------------------------------------------+
Unfortunately, tutor @greenestamps MISSED this error and declared the @josgarithmetic's setup as "fine", instead.
THEREFORE, I came to prevent this huge mistake considering the WRONG setup as a correct.
+-------------------------------------------+
| The correct setup would be AS FOLLOWS |
+-------------------------------------------+
Let x be the Sharon present age.
Then 5 years ago Sharon's age was (x-5) years.
The Kate's age in 5 years will be 90 - (x+5);
hence, the Kate's age 5 years back was (90 - (x+5) - 10) = 80-(x+5) years.
Now we can write equation describing the ratio of their ages 5 years back
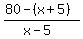 = =  .
Now we can solve it, first cross-multiplying
3*(80-(x+5)) = 4*(x-5)
240 - 3x - 15 = 4x - 20
240 - 15 + 20 = 4x + 3x
245 = 7x
x = 245/7 = 35.
ANSWER. The Sharon's present age is 35 years.
CHECK. In 5 years, Sharon will be 35+5 = 40 years old; Kate will be 90-40 = 50 years old; hence, Kate is 45 years old now.
5 years ago, Sharon was 35-5 = 30 years old, while Kate was 45-5 = 40 years old, and the ratio of their ages 5 years ago was really .
Now we can solve it, first cross-multiplying
3*(80-(x+5)) = 4*(x-5)
240 - 3x - 15 = 4x - 20
240 - 15 + 20 = 4x + 3x
245 = 7x
x = 245/7 = 35.
ANSWER. The Sharon's present age is 35 years.
CHECK. In 5 years, Sharon will be 35+5 = 40 years old; Kate will be 90-40 = 50 years old; hence, Kate is 45 years old now.
5 years ago, Sharon was 35-5 = 30 years old, while Kate was 45-5 = 40 years old, and the ratio of their ages 5 years ago was really 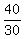 = =  .
The check confirms that my solution is correct. .
The check confirms that my solution is correct.
Solved.
|
|
|