Question 1147611: Matt is half as old as James will be when Matt
is twice as old as James is now. In 5 years,
the sum of Matt and James age will be 100.
How old are Matt and James now?
Found 2 solutions by VFBundy, ikleyn:
Answer by VFBundy(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! Matt's age now = M
James's age now = J
In 5 years, the sum of Matt and James age will be 100.
(M + 5) + (J + 5) = 100
M + J + 10 = 100
M + J = 90
J = 90 - M
So, revised:
Matt's age now = M
James's age now = J = 90 - M
Matt is half as old as James will be when Matt is twice as old as James is now.
Let the period of time "when Matt is twice as old as James now" be equal to X.
Look at the part of the statement where it says: "when Matt is twice as old as James is now."
M + X = 2(90 - M)
M + X = 180 - 2M
3M + X = 180
Now, look at the part of the statement where it says: "Matt is half as old as James will be when..."
M = 0.5(90 - M + X)
M = 45 - 0.5M + 0.5X
1.5M - 0.5X = 45
Now, you have two equations:
3M + X = 180
1.5M - 0.5X = 45
Multiply the second equation by 2:
2(1.5M - 0.5X) = 2(45)
3M - X = 90
Here are your two equations now:
3M + X = 180
3M - X = 90
Add these two equations together and solve for M:
6M = 270
M = 45
From earlier:
Matt's age now = M = 45
James's age now = J = 90 - M = 90 - 45 = 45
So, both men are 45.
========================================================
Check it:
In 5 years, the sum of Matt and James age will be 100.
Both men are 45 now, so in 5 years, both men will be 50. This adds up to 100.
Matt is half as old as James will be when Matt is twice as old as James is now.
To check this, you need to figure out what X is. Take either of our two equations:
3M + X = 180
We know M = 45, so:
3(45) + X = 180
135 + X = 180
X = 45
Let's look at the statement again:
Matt is half as old as James will be when Matt is twice as old as James is now.
"When Matt is twice as old as James is now" happens in 45 years. (Because X = 45.) In 45 years, Matt will be 90 and James is now 45. That's twice as old.
"Matt is half as old as James will be when..." Matt is half as old as James will be WHEN. WHEN is the key word. That WHEN is in 45 years. So, again...Matt is half as old (45) as James will be in 45 years. In 45 years, James will be 90. So, that's half as old.
Answer by ikleyn(52914)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I will try to provide more short solution.
Let x be the Matt's age. Then James' age is 90-x years.
When Matt will be twice as old as James is now ?
- In 2*(90-x)-x years, which is 180-3x years.
What will be the James' age in 180-3x years ?
- James age will be (90-x) + (180-3x), or, after simplifying, (270-4x) years.
Then the condition says
x = 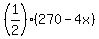 It is your basic equation to the problem. Now your task is to solve it.
2x = 270 - 4x
6x = 270
x = 270/6 = 45.
ANSWER. Matt is 45 years old. James is 90-45 = 45 years old, too.
CHECK. When Matt will be twice as old as James is now (i.e. as old as 2*45 = 90 years ?
- In 90-45 = 45 years.
What will be James' age in 45 years ?
- it will be 45 + 45 = 90.
45 =
It is your basic equation to the problem. Now your task is to solve it.
2x = 270 - 4x
6x = 270
x = 270/6 = 45.
ANSWER. Matt is 45 years old. James is 90-45 = 45 years old, too.
CHECK. When Matt will be twice as old as James is now (i.e. as old as 2*45 = 90 years ?
- In 90-45 = 45 years.
What will be James' age in 45 years ?
- it will be 45 + 45 = 90.
45 = 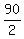 . ! Correct ! . ! Correct !
Solved.
----------------
In such problems, than shorter, compact and straightforward the solution is, than more (and better) it is understandable.
/\/\/\/\/\/\/\/
In this site, there is a bunch of age word problems
- Age problems and their solutions
- A fresh formulation of a traditional age problem
- Really intricate age word problem (*)
- Selected age word problems from the archive
- Age problems for mental solution
- One unusual age word problem
- Age problems with a defective sum of ages
- OVERVIEW of lessons on age problems
Of them, the problem marked (*) in the list is very close to the given problem.
Read the lessons and become an expert in solving age problems (!)
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Age word problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|