SOLUTION: Tickets for a film show were sold at ghc5 per adult and ghc3 per child. The total amount raised from the 500 tickets sold was ghc2300. Find the number of adults who bought the tick

Click here to see ALL problems on Age Word Problems

Question 1144151: Tickets for a film show were sold at ghc5 per adult and ghc3 per child. The total amount raised from the 500 tickets sold was ghc2300. Find the number of adults who bought the tickets for the show.

Found 3 solutions by josgarithmetic, greenestamps, ikleyn:
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website!
----------------------------------------------
ghc5 per adult and ghc3 per child. The total amount raised from the 500 tickets sold was ghc2300. Find the number of adults
--------------------------------------------------

y adults
500-y children

.
.

Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

This is classic kind of problem for teaching students how to solve problems using algebra. Another tutor has shown you one way to set up the problem to solve using algebra.

Here is a method for solving any of these kinds of "mixture" problems that uses only logical reasoning and some simple arithmetic. If you understand how to use it, it will get you to the answer much faster and with far less work than an algebraic solution.

And if your mental arithmetic is good, you won't need pencil and paper to solve the problem.

Here is the process for this problem.

(1) 500 tickets all at ghc3 would bring in ghc1500; 500 all at ghc5 would bring in ghc2500. The actual total was ghc2300.

(2) ghc2300 is 4/5 of the way from ghc1500 to ghc2500. (Picture the three numbers 1500, 2300, and 2500 on a number line; 2300 is 4/5 of the way from 1500 to 2500.)

(3) That means 4/5 of the tickets were the higher price adult tickets.

ANSWER: 4/5 of the 500 tickets, or 400 tickets, were adult tickets at ghc5 each.

Answer by ikleyn(52790)   (Show Source):
You can put this solution on YOUR website!
.

        There are different methods to solve such problems.
        I will show you several basic methods in this post.

                Solution 1   (the system of 2 equations approach)

Let x be the number of the adult tickets and let y be the number of the child tickets. Then you have these two equations x + y = 500, (1) (counting tickets) 5x + 3y = 2300 ghc (2) (counting revenue in ghc) They are your basic equations, and as soon as you got this system, the setup is completed. There are different methods of solving such systems (Substitution, Elimination, using determinants). I will use the Substitution method here. From equation (1) express y = 500-x and substitute it into equation (2). You will get a single equation for the unknown x 5x + 3(500-x) = 2300. (3) 5x + 3*500 - 3x = 1142 ====> (5-3)x = 2300 - 3*500 ====> x = 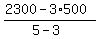= 400. (4) Thus, 400 adult tickets were sold. Hence the number of the child tickets was 500 - 400 = 100. Check. 5*400 + 3*100 = 2300 ghc. ! Correct. ! Answer. 400 adult tickets.

                Solution 2   (one equation approach)

Let x be the number of adult tickets (the unknown value under the question) Then the number of the child tickets is (500-x), according to the condition. The adult tickets cost 5x ghc. The child tickets cost 3*(500-x) ghc. Summing up these money, you get the revenue equation 5x + 3*(500-x) = 2300. (5) It is your basic equation in the frame of this approach, and as soon as you got this equation, the setup is completed. Notice that this equation (5) coincides exactly with the equation (3) of the solution 1 above. Solve equation (5) by the same method as it was done in the Solution 1. Surely, you will get the same answer: the number of adult tickets is 400.

                Solution 3   (Logical analysis)

Let assume for a minute that all 500 tickets were child tickets. Then the total revenue would be 3*500 = 1500 ghc. It is by 2300 - 1500 = 800 ghc less than the given revenue value. Why did we get the difference ? - But of course, because we counted all tickets as the child tickets. To compensate the difference, we must replace some number of 500 child tickets by the adult tickets in our analysis. At each replacement, we diminish the difference of 800 ghc by 2 ghc (which is the difference 5 ghc - 3 ghc between the adult and the child tickets price). Then it is clear that the number of adult tickets is 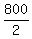= 400. Thus logical solution is completed, and you obtain the same answer. 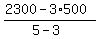Notice, that this logic works EXACTLY in accordance with the formula number of adult tickets = (6) which is EXACTLY THE SAME as the formula (4).

--------------

Congratulations !   You are now familiar with 3 methods for ticket problems solution.

I suggest that algebraic methods will be your basic methods for such problems,
and the logical analysis method will allow you to solve the problems QUICKLY without using equations.
I will be happy if it will make your horizon wider.

--------------

To see other similar solved problems on tickets, look into the lessons
    - Using systems of equations to solve problems on tickets
    - Three methods for solving standard (typical) problems on tickets
in this site.

To see how the logical method works for other similar problems, look into the lessons
    - Problem on two-wheel and three-wheel bicycles
    - Problem on animals at a farm
    - Problem on pills in containers
    - What type of problems are these?
in this site.

================

The lesson to learn from my presentation :

The typical ticket problem is THIS : - You are given the total number of cheap and expensive tickets; - you are given the prices for tickets of these two categories; - you are given the total revenue; - you are asked to find the number of tickets in each of the two categories. When you solve such a problem, you may use ANY of the three methods of this presentation. But you also can write the solution for the number of more expensive tickets in one line as a fraction whose numerator is the difference between the given revenue and the hypothetical revenue assuming that all tickets are for cheap price, and whose denominator is the difference (positive difference) between expensive and cheap prices. The logic explained in the Solution 3 will help you to go in this way and will prevent you of making errors or steps aside. And when the formula is implemented and all the given numbers are plug-in, all you need to do is to copy and paste the formula into MS Excel in your computer (or into other similar software) and press the "Enter" button to get the final number (solution; answer). And it is, if you want, the fourth method of solving such problems - the shortest and the quickest.

Come again to this forum to learn more !