ten yrs. ago, mike was four times as old as liza. Now he is only twice as old as Liza. How old are they now?
-------------
Ten years ago, Mike was four times as old as Liza. Now he is only twice as old as Liza. How old are they now?
-------------
Let M=Mike's age, and L=Liza's age
M = 2L (1) (from "Now he is only twice as old as Liza")
M-10 = 4(L-10) (2) (from "Ten years ago, Mike was four times as old as Liza.")
There are several approaches to solve this system of equations. You couild subsititue 2L for M (specified by equation(1)) into (2). You could also subtract the entire equation (2) from equation (1). A third option is to set up a matrix and find its inverse, then use that inverse to solve: for [A][x]=[b] find [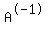
] then [x] = [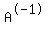][b]
Substitution:
(1) says M=2L so we can write (2) as:
2L-10 = 4(L-10)
2L-10 = 4L-40 distributed the 4 into parenthesis
30 = 2L subtracted 2L from each side, added 40 to each side
15 = L divided each side by 2
L=15 tells us M=30 (by plugging L=15 into (1))
Subtraction of equations:
(1) - (2) gives:
M-(M-10) = 2L-4(L-10)
M-M+10 = 2L-4L+40
10 = -2L+40
-30 = -2L
15 = L (same result as substitution, as expected)
The matrix method comes from Linear Algebra:
(1) can be written 2L - M = 0
(2) can be written 4L - M = 30
Taking the coefficients we can form the matrix equation:
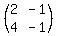x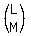 
= 
One would then find the inverse of the 2x2 matrix and that inverse, multiplied by the right hand side gives the answer.
The inverse of 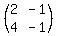is 
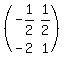
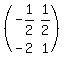= x = 
= 
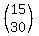---> L=15, M=30
------------
Check:
L=15, M=30, obviously now Mike is twice as old as Liza. But let's check their ages 10 years ago:
Liza was 15-10 = 5
Mike was 30-10 = 20 (20 is 4*5 so this checks out).
