SOLUTION: Tom is 2 years older than his brother. the product of their ages 6 years from now will be 120 more than the product of their present ages. Find each of their ages

The condition gives you two equations

T - B = 2,                  (1)
(T+6)*(B+6) - T*B = 120.    (2)


Simplify eq(2):

T*B + 6B + 6T + 36 - T*B = 120,

6B + 6T = 120 - 36 = 84,

T + B = 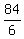 = 14.


Thus the modified system of equation is THIS:

T - B =  2                   (3)
T + B = 14                   (4)


Add the equations (3) and (4). You will get

2T = 2 + 14 = 16.   Hence,  T =  = 8.


Then from (4),  B = 14 - T = 14 - 8 = 6.


Answer.  Tom is 8 years old.  His brother is 6 years old.


Check.   (8+6)*(6+6) - 8*6 = 120.   ! Correct !