Question 1096882: Teresa is 6 years older than ann. In 4 years, the sum of their age will be 66. Find Teresa's present age.
Found 4 solutions by Alan3354, josgarithmetic, MathTherapy, ikleyn:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Teresa is 6 years older than ann. In 4 years, the sum of their age will be 66. Find Teresa's present age.
--------------
Step 1, find the sum of their ages now.
==============
What is "present age?"
How does that differ from age?
--------
What is your age? vs. What is your present age?
--------
People like to add words, think it makes them appear smart. It doesn't, just the opposite.
-----------
eg, "What's your current location?" vs. "Where are you?"
Answer by josgarithmetic(39620)  (Show Source):
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! Teresa is 6 years older than ann. In 4 years, the sum of their age will be 66. Find Teresa's present age.
Teresa's AGE is good enough. Current is UNNECESSARY, as explained by Alan.
FYI: Teresa can NEVER be 22, as suggested by "you know who," so as usual, IGNORE, IGNORE, IGNORE!
Answer by ikleyn(52802)  (Show Source):
You can put this solution on YOUR website! .
Solution 1
Directly from the condition, you have this system of 2 equations in 2 unknowns:
T - A = 6 (1) ("Teresa is 6 years older than Ann.")
(T+4) + (A+4) = 66 (2) ("In 4 years")
Simplify:
T - A = 6, (1')
T + A = 58. (2')
Add the equations 1') and (2') (both sides). You will get
2T = 6+58 = 64 ====> T = 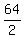 = 32.
Answer. Teresa is 32 years old.
Solution 2
A = T - 6,
(T+4) + (A+4) = 66.
Replace A in the last equation by (T-6) based on the previous equation. You will get
(T+4) + ((T-6)+4) = 66.
You have a single equation for unknown T. Simplify and solve for T.
T + 4 + T - 6 + 4 = 66 ====>
2T + 2 = 66 ====> 2T = 66-2 = 64 ====> T = 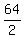= 32.
You got the same answer.
----------------
There is a bunch of lessons on age word problems
- Age problems and their solutions
- A fresh formulation of a traditional age problem
- Really intricate age word problem
- Selected age word problems from the archive
- Age problems for mental solution
in this site.
Read them and become an expert in solving age problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Age word problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|
